MAXimal

добавлено: 10 Jun 2009 21:03
редактировано: 24 May 2016 5:41

Поток минимальной стоимости, циркуляция минимальной стоимости. Алгоритм удаления циклов отрицательного веса

Постановка задач

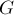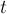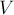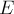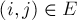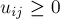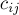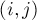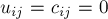Пусть $G$ — сеть (network), то есть ориентированный граф, в котором выбраны вершины-исток $s$ и сток $t$ . Множество вершин обозначим через $V$ , множество рёбер — через $E$ . Каждому ребру $(i,j) \in E$ сопоставлены его пропускная способность $u_{ij} \ge 0$ и стоимость единицы потока $c_{ij}$ . Если какого-то ребра $(i,j)$ в графе нет, то предполагается, что $u_{ij} = c_{ij} = 0$ .

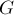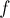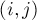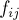Потоком (flow) в сети $G$ называется такая действительнозначная функция $f$ , сопоставляющая каждой паре вершин $(i,j)$ поток $f_{ij}$ между ними, и удовлетворяющая трём условиям:

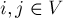Ограничение пропускной способности (выполняется для любых $i, j \in V$ ):
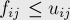
$f_{ij} \le u_{ij}$
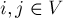Антисимметричность (выполняется для любых $i, j \in V$ ):
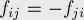
$f_{ij} = - f_{ji}$
Сохранение потока (выполняется для любых 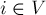$i \in V$ , кроме $i=s$ , $i=t$ ):
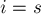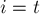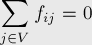
$\sum_{j \in V} f_{ij} = 0$

Величиной потока называется величина

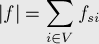
$|f| = \sum_{i \in V} f_{si}$

Стоимостью потока называется величина

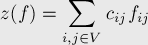
$z(f) = \sum_{i,j \in V} c_{ij} f_{ij}$

Задача нахождения потока минимальной стоимости заключается в том, что по заданной величине потока 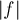$|f|$ требуется найти поток, обладающий минимальной стоимостью 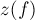$z(f)$ . Стоит обратить внимание на то, что стоимости 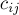$c_{ij}$ , приписанные рёбрам, отвечают за стоимость единицы потока вдоль этого ребра; иногда встречается задача, когда рёбрам сопоставляются стоимости протекания потока вдоль этого ребра (т.е. если протекает поток любой величины, то взимается эта стоимость, независимо от величины потока) — эта задача не имеет ничего общего с рассматриваемой здесь и, более того, является NP-полной.

Задача нахождения максимального потока минимальной стоимости заключается в том, чтобы найти поток наибольшей величины, а среди всех таких — с минимальной стоимостью. В частном случае, когда веса всех рёбер одинаковы, эта задача становится эквивалентной обычной задаче о максимальном потоке.

Задача нахождения циркуляции минимальной стоимости заключается в том, чтобы найти поток нулевой величины с минимальной стоимостью. Если все стоимости неотрицательные, то, понятно, ответом будет нулевой поток 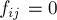$f_{ij}=0$ ; если же есть рёбра отрицательного веса (а, точнее, циклы отрицательного веса), то даже при нулевом потоке возможно найти поток отрицательной стоимости. Задачу нахождения циркуляции минимальной стоимости можно, разумеется, поставить и на сети без истока и стока, поскольку никакой смысловой нагрузки они не несут (впрочем, в такой граф можно добавить исток и сток в виде изолированных вершин и получить обычную по формулировке задачу). Иногда ставится задача нахождения циркуляции максимальной стоимости — понятно, достаточно изменить стоимости рёбер на противоположные и получим задачу нахождения циркуляции уже минимальной стоимости.

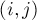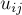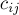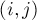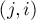Все эти задачи, разумеется, можно перенести и на неориентированные графы. Впрочем, перейти от неориентированного графа к ориентированному легко: каждое неориентированное ребро $(i,j)$ с пропускной способностью $u_{ij}$ и стоимостью $c_{ij}$ следует заменить двумя ориентированными рёбрами $(i,j)$ и $(j,i)$ с одинаковыми пропускными способностями и стоимостями.

Остаточная сеть

Концепция остаточной сети 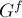$G^f$ основана на следующей простой идее. Пусть есть некоторый поток 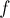$f$ ; вдоль каждого ребра 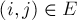$(i,j) \in E$ протекает некоторый поток 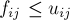$f_{ij} \le u_{ij}$ . Тогда вдоль этого ребра можно (теоретически) пустить ещё 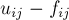$u_{ij} - f_{ij}$ единиц потока; эту величину и назовём остаточной пропускной способностью:

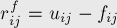
$r_{ij}^f = u_{ij} - f_{ij}$

Стоимость этих дополнительных единиц потока будет такой же:

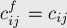
$c_{ij}^f = c_{ij}$

Однако помимо этого, прямого ребра 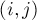$(i,j)$ , в остаточной сети 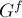$G^f$ появляется и обратное ребро 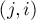$(j,i)$ . Интуитивный смысл этого ребра в том, что мы можем в будущем отменить часть потока, протекавшего по ребру 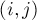$(i,j)$ . Соответственно, пропускание потока вдоль этого обратного ребра 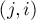$(j,i)$ фактически, и формально, означает уменьшение потока вдоль ребра 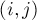$(i,j)$ . Обратное ребро имеет пропускную способность, равную нулю (чтобы, например, при 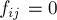$f_{ij}=0$ и по обратному ребру невозможно было бы пропустить поток; при положительной величине 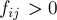$f_{ij}>0$ для обратного ребра по свойству антисимметричности станет 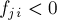$f_{ji}<0$ , что меньше 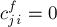$c_{ji}^f = 0$ , т.е. можно будет пропускать какой-то поток вдоль обратного ребра), остаточную пропускную способность — равную потоку вдоль прямого ребра, а стоимость — противоположную (ведь после отмены части потока мы должны соответственно уменьшить и стоимость):

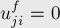
$u_{ji}^f = 0$
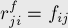
$r_{ji}^f = f_{ij}$
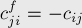
$c_{ji}^f = -c_{ij}$

Таким образом, каждому ориентированному ребру в 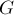$G$ соответствует два ориентированных ребра в остаточной сети 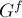$G^f$ , и у каждого ребра остаточной сети появляется дополнительная характеристика — остаточная пропускная способность. Впрочем, нетрудно заметить, что выражения для остаточной пропускной способности 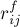$r_{ij}^f$ по сути одинаковы как для прямого, так и для обратного ребра, т.е. мы можем записать для любого ребра 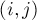$(i,j)$ остаточной сети:

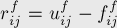
$r_{ij}^f = u_{ij}^f - f_{ij}^f$

Кстати, при реализации это свойство позволяет не хранить остаточные пропускные способности, а просто вычислять их при необходимости для ребра.

Следует отметить, что из остаточной сети удаляются все рёбра, имеющие нулевую остаточную пропускную способность. Остаточная сеть 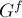$G^f$ должна содержать только рёбра с положительной остаточной пропускной способностью $r_{ij}^f$ .

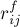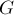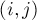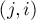Здесь стоит обратить внимание на такой важный момент: если в сети $G$ были одновременно оба ребра $(i,j)$ и $(j,i)$ , то в остаточной сети у каждого из них появится по обратному ребру, и в итоге появятся кратные рёбра. Например, такая ситуация часто возникает, когда сеть строится по неориентированному графу (и, получается, каждое неориентированное ребро в итоге приведёт к появлению четырёх рёбер в остаточной сети). Эту особенность нужно всегда помнить, она приводит к небольшому усложнению программирования, хотя в общем ничего не меняет. Кроме того, обозначение ребра 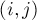$(i,j)$ в таком случае становится неоднозначным, поэтому ниже мы везде будем считать, что такой ситуации в сети нет (исключительно в целях простоты и корректности описаний; на правильность идей это никак не влияет).

Критерий оптимальности по наличию циклов отрицательного веса

Теорема. Некоторый поток 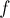$f$ является оптимальным (т.е. имеет наименьшую стоимость среди всех потоков такой же величины) тогда и только тогда, когда остаточная сеть 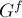$G^f$ не содержит циклов отрицательного веса.

Доказательство: необходимость. Пусть поток 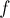$f$ является оптимальным. Предположим, что остаточная сеть 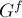$G^f$ содержит цикл отрицательного веса. Возьмём этот цикл отрицательного веса и выберем минимум $k$ среди остаточных пропускных способностей рёбер этого цикла ( $k$ будет больше нуля). Но тогда можно увеличить поток вдоль каждого ребра цикла на величину $k$ , при этом никакие свойства потока не нарушатся, величина потока не изменится, однако стоимость потока уменьшится (уменьшится на стоимость цикла, умноженную на $k$ ). 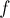Таким образом, если есть цикл отрицательного веса, то $f$ не может быть оптимальным, ч.т.д.

Доказательство: достаточность. Для этого сначала докажем вспомогательные факты.

Лемма 1 (о декомпозиции потока): любой поток 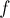$f$ можно представить в виде совокупности путей из истока в сток и циклов, все — имеющие положительный поток. Докажем эту лемму конструктивно: покажем, как разбить поток на совокупность путей и циклов. Если поток имеет ненулевую величину, то, очевидно, из истока $s$ выходит хотя бы одно ребро с положительным потоком; пройдём по этому ребру, окажемся в какой-то вершине $v_1$ . 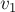Если эта вершина 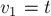$v_1 = t$ , то останавливаемся — нашли путь из $s$ в $t$ . 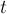Иначе, по свойству сохранения потока, из 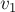$v_1$ должно выходить хотя бы одно ребро с положительным потоком; пройдём по нему в какую-то вершину 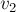$v_2$ . Повторяя этот процесс, мы либо придём в сток 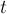$t$ , либо же придём в какую-то вершину во второй раз. 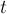В первом случае мы обнаружим путь из $s$ в $t$ , во втором — цикл. Найденный путь/цикл будет иметь положительный поток $k$ (минимум из потоков рёбер этого пути/цикла). Тогда уменьшим поток вдоль каждого ребра этого пути/цикла на величину $k$ , в результате получим снова поток, к которому снова применим этот процесс. Рано или поздно поток вдоль всех рёбер станет нулевым, и мы найдём его декомпозицию на пути и циклы.

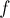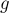Лемма 2 (о разности потоков): для любых двух потоков $f$ и $g$ одной величины ( 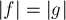$|f| = |g|$ ) поток 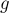$g$ можно представить как поток 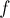$f$ плюс несколько циклов в остаточной сети 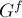$G^f$ . Действительно, рассмотрим разность этих потоков 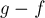$g-f$ (вычитание потоков — это почленное вычитание, т.е. вычитание потоков вдоль каждого ребра). Нетрудно убедиться, что в результате получится некоторый поток нулевой величины, т.е. циркуляция. Произведём декомпозицию этой циркуляции согласно предыдущей лемме. Очевидно, это декомпозиция не может содержать путей (т.к. наличие 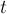$s$ - $t$ -пути с положительным потоком означает, что и величина потока в сети положительна). 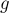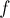Таким образом, разность потоков $g$ и $f$ можно представить в виде суммы циклов в сети 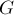$G$ . Более того, это будут и циклы в остаточной сети 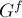$G^f$ , т.к. 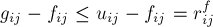$g_{ij} - f_{ij} \le u_{ij} - f_{ij} = r_{ij}^f$ , ч.т.д.

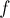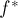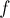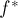Теперь, вооружившись этими леммами, мы легко можем доказать достаточность. Итак, рассмотрим произвольный поток $f$ , в остаточной сети которого нет циклов отрицательной стоимости. Рассмотрим также поток той же величины, но минимальной стоимости $f^*$ ; докажем, что $f$ и $f^*$ имеют одинаковую стоимость. Согласно лемме 2, поток 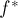$f^*$ можно представить в виде суммы потока 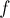$f$ и нескольких циклов. Но раз стоимости всех циклов неотрицательны, то и стоимость потока 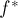$f^*$ не может быть меньше стоимости потока 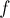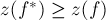$f$ : $z(f^*) \ge z(f)$ . С другой стороны, т.к. поток 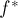$f^*$ является оптимальным, то его стоимость не может быть выше стоимости потока 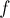$f$ . Таким образом, 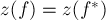$z(f) = z(f^*)$ , ч.т.д.

Алгоритм удаления циклов отрицательного веса

Только что доказанная теорема даёт нам простой алгоритм, позволяющий найти поток минимальной стоимости: если у нас есть какой-то поток 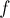$f$ , то построить для него остаточную сеть, проверить, есть ли в ней цикл отрицательного веса. Если такого цикла нет, то поток 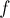$f$ является оптимальным (имеет наименьшую стоимость среди всех потоков такой же величины). Если же был найден цикл отрицательной стоимости, то посчитать поток $k$ , который можно пропустить дополнительно через этот цикл (это $k$ будет равно минимуму из остаточных пропускных способностей рёбер цикла). 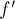Увеличив поток на $k$ вдоль каждого ребра цикла, мы, очевидно, не нарушим свойства потока, не изменим величину потока, но уменьшим стоимость этого потока, получив новый поток $f^\prime$ , для которого надо повторить весь процесс.

Таким образом, чтобы запустить процесс улучшения стоимости потока, нам предварительно нужно найти произвольный поток нужной величины (каким-нибудь стандартным алгоритмом нахождения максимального потока, см., например, алгоритм Эдмондса-Карпа). В частности, если требуется найти циркуляцию наименьшей стоимости, то начать можно просто с нулевого потока.

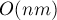Оценим асимптотику алгоритма. Поиск цикла отрицательной стоимости в графе с $n$ вершинами и $m$ рёбрами производится за $O(nm)$ (см. соответствующую статью). Если мы обозначим через 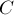$C$ наибольшее из стоимостей рёбер, через 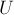$U$ — наибольшую из пропускных способностей, то максимальное значение стоимости потока не превосходит 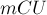$mCU$ . Если все стоимости и пропускные способности — целые числа, то каждая итерация алгоритма уменьшает стоимость потока как минимум на единицу; следовательно, всего алгоритм совершит 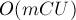$O(mCU)$ итераций, а итоговая асимптотика составит:

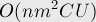
$O(nm^2CU)$

Эта асимптотика — не строго полиномиальна (strong polynomial), поскольку зависит от величин пропускных способностей и стоимостей.

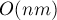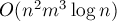Впрочем, если искать не произвольный отрицательный цикл, а использовать какой-то более чёткий подход, то асимптотика может значительно уменьшиться. Например, если каждый раз искать цикл с минимальной средней стоимостью (что также можно производить за $O(nm)$ ), то время работы всего алгоритма можно оценить строго полиномиальной асимптотикой $O(n^2 m^3 \log n)$ .

Реализация

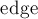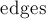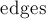Сначала введём структуры данных и функции для хранения графа. Каждое ребро хранится в отдельной структуре $\rm edge$ , все рёбра лежат в общем списке $\rm edges$ , а для каждой вершины $i$ в векторе ${\rm g}[i]$ хранятся номера рёбер, выходящих из неё. Такая организация позволяет легко находить номер обратного ребра по номеру прямого ребра — они оказываются в списке $\rm edges$ соседними, и номер одного можно получить по номеру другого операцией "^1" (она инвертирует младший бит). Добавление ориентированного ребра в граф осуществляет функция 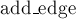$\rm add\_edge$ , которая добавляет сразу прямое и обратное рёбра.

const int MAXN = 100*2;
int n;
struct edge {
	int v, to, u, f, c;
};
vector<edge> edges;
vector<int> g[MAXN];
 
void add_edge (int v, int to, int cap, int cost) {
	edge e1 = { v, to, cap, 0, cost };
	edge e2 = { to, v, 0, 0, -cost };
	g[v].push_back ((int) edges.size());
	edges.push_back (e1);
	g[to].push_back ((int) edges.size());
	edges.push_back (e2);
}

В основной программе после чтения графа идёт бесконечный цикл, внутри которого выполняется алгоритм Форда-Беллмана, и если он обнаруживает цикл отрицательной стоимости, то вдоль этого цикла увеличивается поток. Поскольку остаточная сеть может представлять собой несвязный граф, то алгоритм Форда-Беллмана запускается из каждой не достигнутой ещё вершины. В целях оптимизации алгоритм использует очередь (текущая очередь 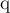$\rm q$ и новая очередь 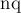$\rm nq$ ), чтобы не перебирать на каждой стадии все рёбра. Вдоль обнаруженного цикла каждый раз проталкивается ровно единица потока, хотя, понятно, в целях оптимизации величину потока можно определять как минимум остаточных пропускных способностей.

const int INF = 1000000000;
for (;;) {
	bool found = false;
 
	vector<int> d (n, INF);
	vector<int> par (n, -1);
	for (int i=0; i<n; ++i)
		if (d[i] == INF) {
			d[i] = 0;
			vector<int> q, nq;
			q.push_back (i);
			for (int it=0; it<n && q.size(); ++it) {
				nq.clear();
				sort (q.begin(), q.end());
				q.erase (unique (q.begin(), q.end()), q.end());
				for (size_t j=0; j<q.size(); ++j) {
					int v = q[j];
					for (size_t k=0; k<g[v].size(); ++k) {
						int id = g[v][k];
						if (edges[id].f < edges[id].u)
							if (d[v] + edges[id].c < d[edges[id].to]) {
								d[edges[id].to] = d[v] + edges[id].c;
								par[edges[id].to] = v;
								nq.push_back (edges[id].to);
							}
					}
				}
				swap (q, nq);
			}
			if (q.size()) {
				int leaf = q[0];
				vector<int> path;
				for (int v=leaf; v!=-1; v=par[v])
					if (find (path.begin(), path.end(), v) == path.end())
						path.push_back (v);
					else {
						path.erase (path.begin(), find (path.begin(), path.end(), v));
						break;
					}
				for (size_t j=0; j<path.size(); ++j) {
					int to = path[j],  v = path[(j+1)%path.size()];
					for (size_t k=0; k<g[v].size(); ++k)
						if (edges[ g[v][k] ].to == to) {
							int id = g[v][k];
							edges[id].f += 1;
							edges[id^1].f -= 1;
						}
				}
				found = true;
			}
		}
 
	if (!found)  break;
}

Литература

Томас Кормен, Чарльз Лейзерсон, Рональд Ривест, Клиффорд Штайн. Алгоритмы: Построение и анализ [2005]
Ravindra Ahuja, Thomas Magnanti, James Orlin. Network flows [1993]
Andrew Goldberg, Robert Tarjan. Finding Minimum-Cost Circulations by Cancelling Negative Cycles [1989]