Нахождение отрицательного цикла в графе

Дан ориентированный взвешенный граф 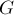$G$ с $n$ вершинами и $m$ рёбрами. Требуется найти в нём любой цикл отрицательного веса, если таковой имеется.

При другой постановке задачи — требуется найти все пары вершин такие, что между ними существует путь сколько угодно малой длины.

Эти два варианта задачи удобно решать разными алгоритмами, поэтому ниже будут рассмотрены оба из них.

Одна из распространённых "жизненных" постановок этой задачи — следующая: известны курсы валют, т.е. курсы перевода из одной валюты в другую. Требуется узнать, можно ли некоторой последовательностью обменов получить выгоду, т.е. стартовав с одной единицы какой-либо валюты, получить в итоге больше чем одну единицу этой же валюты.

Решение с помощью алгоритма Форда-Беллмана

Алгоритм Форда-Беллмана позволяет проверить наличие или отсутствие цикла отрицательного веса в графе, а при его наличии — найти один из таких циклов.

Не будем вдаваться здесь в подробности (которые описаны в статье по алгоритму Форда-Беллмана), а приведём лишь итог — то, как работает алгоритм.

Делается $n$ итераций алгоритма Форда-Беллмана, и если на последней итерации не произошло никаких изменений — то отрицательного цикла в графе нет. В противном случае возьмём вершину, расстояние до которой изменилось, и будем идти от неё по предкам, пока не войдём в цикл; этот цикл и будет искомым отрицательным циклом.

Реализация:

struct edge {
	int a, b, cost;
};
 
int n, m;
vector<edge> e;
const int INF = 1000000000;
 
void solve() {
	vector<int> d (n);
	vector<int> p (n, -1);
	int x;
	for (int i=0; i<n; ++i) {
		x = -1;
		for (int j=0; j<m; ++j)
			if (d[e[j].b] > d[e[j].a] + e[j].cost) {
				d[e[j].b] = max (-INF, d[e[j].a] + e[j].cost);
				p[e[j].b] = e[j].a;
				x = e[j].b;
			}
	}
 
	if (x == -1)
		cout << "No negative cycle found.";
	else {
		int y = x;
		for (int i=0; i<n; ++i)
			y = p[y];
 
		vector<int> path;
		for (int cur=y; ; cur=p[cur]) {
			path.push_back (cur);
			if (cur == y && path.size() > 1)  break;
		}
		reverse (path.begin(), path.end());
 
		cout << "Negative cycle: ";
		for (size_t i=0; i<path.size(); ++i)
			cout << path[i] << ' ';
	}
}

Решение с помощью алгоритма Флойда-Уоршелла

Алгоритм Флойда-Уоршелла позволяет решать вторую постановку задачи — когда надо найти все пары вершин 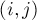$(i,j)$ , между которыми кратчайшего пути не существует (т.е. он имеет бесконечно малую величину).

Опять же, более подробные объяснения содержатся в описании алгоритма Флойда-Уоршелла, а здесь мы приведём только итог.

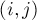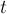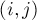После того, как алгоритм Флойда-Уоршелла отработает для входного графа, переберём все пары вершин $(i,j)$ , и для каждой такой пары проверим, бесконечно мал кратчайший путь из $i$ в $j$ или нет. Для этого переберём третью вершину $t$ , и если для неё оказалось $d[t][t]<0$ (т.е. она лежит в цикле отрицательного веса), а сама она достижима из $i$ и из неё достижима $j$ — то путь $(i,j)$ может иметь бесконечно малую длину.

Реализация:

for (int i=0; i<n; ++i)
	for (int j=0; j<n; ++j)
		for (int t=0; t<n; ++t)
			if (d[i][t] < INF && d[t][t] < 0 && d[t][j] < INF)
				d[i][j] = -INF;

Задачи в online judges

Список задач, в которых требуется искать цикл отрицательного веса: