MAXimal
добавлено: 22 Jun 2008 13:37
редактировано: 1 Oct 2012 12:46
Содержание [скрыть]
Суффиксный массив
Дана строка ![s[0 \ldots n-1]](../tex2png/cache/0697d6e9689fa1f0f0cf71d3a81c61e0.png) длины
длины  .
.
 -ым суффиксом строки называется подстрока
-ым суффиксом строки называется подстрока ![s[i \ldots n-1]](../tex2png/cache/85e46e70be2dd41f5bf34c3be9ad6c6a.png) ,
, 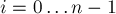 .
.
Тогда суффиксным массивом строки  называется перестановка индексов суффиксов
называется перестановка индексов суффиксов ![p[0 \ldots n-1]](../tex2png/cache/9ff50b5f8fed0fbedd5d2edbbbd08679.png) ,
, ![p[i] \in [0;n-1]](../tex2png/cache/e8f4fad19b8d85ed98637540f6e69db3.png) , которая задаёт порядок суффиксов в порядке лексикографической сортировки. Иными словами, нужно выполнить сортировку всех суффиксов заданной строки.
, которая задаёт порядок суффиксов в порядке лексикографической сортировки. Иными словами, нужно выполнить сортировку всех суффиксов заданной строки.
Например, для строки 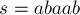 суффиксный массив будет равен:
суффиксный массив будет равен:
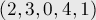
Построение за 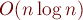
Строго говоря, описываемый ниже алгоритм будет выполнять сортировку не суффиксов, а циклических сдвигов строки. Однако из этого алгоритма легко получить и алгоритм сортировки суффиксов: достаточно приписать в конец строки произвольный символ, который заведомо меньше любого символа, из которого может состоять строка (например, это может быть доллар или шарп; в языке C в этих целях можно использовать уже имеющийся нулевой символ).
Сразу заметим, что поскольку мы сортируем циклические сдвиги, то и подстроки мы будем рассматривать циклические: под подстрокой ![s[i \ldots j]](../tex2png/cache/1da9aede35685d45e082c44a363fe070.png) , когда
, когда 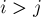 , понимается подстрока
, понимается подстрока ![s[i \ldots n-1] + s[0 \ldots j]](../tex2png/cache/c6ae5521942d8312724f71a41cf27571.png) . Кроме того, предварительно все индексы берутся по модулю длины строки (в целях упрощения формул я буду опускать явные взятия индексов по модулю).
. Кроме того, предварительно все индексы берутся по модулю длины строки (в целях упрощения формул я буду опускать явные взятия индексов по модулю).
Рассматриваемый нами алгоритм состоит из примерно 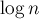 фаз. На
фаз. На  -ой фазе (
-ой фазе (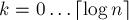 ) сортируются циклические подстроки длины
) сортируются циклические подстроки длины 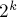 . На последней,
. На последней, 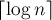 -ой фазе, будут сортироваться подстроки длины
-ой фазе, будут сортироваться подстроки длины 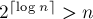 , что эквивалентно сортировке циклических сдвигов.
, что эквивалентно сортировке циклических сдвигов.
На каждой фазе алгоритм помимо перестановки ![p[0 \ldots n-1]](../tex2png/cache/9ff50b5f8fed0fbedd5d2edbbbd08679.png) индексов циклических подстрок будет поддерживать для каждой циклической подстроки, начинающейся в позиции
индексов циклических подстрок будет поддерживать для каждой циклической подстроки, начинающейся в позиции  с длиной
с длиной 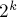 , номер
, номер ![c[i]](../tex2png/cache/f32ed290849269d380c1c6a66e03871d.png) класса эквивалентности, которому эта подстрока принадлежит. В самом деле, среди подстрок могут быть одинаковые, и алгоритму понадобится информация об этом. Кроме того, номера
класса эквивалентности, которому эта подстрока принадлежит. В самом деле, среди подстрок могут быть одинаковые, и алгоритму понадобится информация об этом. Кроме того, номера ![c[i]](../tex2png/cache/f32ed290849269d380c1c6a66e03871d.png) классов эквивалентности будем давать таким образом, чтобы они сохраняли и информацию о порядке: если один суффикс меньше другого, то и номер класса он должен получить меньший. Классы будем для удобства нумеровать с нуля. Количество классов эквивалентности будем хранить в переменной
классов эквивалентности будем давать таким образом, чтобы они сохраняли и информацию о порядке: если один суффикс меньше другого, то и номер класса он должен получить меньший. Классы будем для удобства нумеровать с нуля. Количество классов эквивалентности будем хранить в переменной 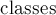 .
.
Приведём пример. Рассмотрим строку 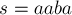 . Значения массивов
. Значения массивов ![p[]](../tex2png/cache/f41743bb1304c4dfaee1474862f9de80.png) и
и ![c[]](../tex2png/cache/d9e2aa831637d909843d3ec6bd160813.png) на каждой стадии с нулевой по вторую таковы:
на каждой стадии с нулевой по вторую таковы:
![\matrix{
0: & p=(0,1,3,2) & c=(0,0,1,0) \cr
1: [...]](../tex2png/cache/b552590d87133a6efaf56d021b120bf7.png)
Стоит отметить, что в массиве ![p[]](../tex2png/cache/f41743bb1304c4dfaee1474862f9de80.png) возможны неоднозначности. Например, на нулевой фазе массив мог равняться:
возможны неоднозначности. Например, на нулевой фазе массив мог равняться: 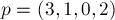 . То, какой именно вариант получится, зависит от конкретной реализации алгоритма, но все варианты одинаково правильны. В то же время, в массиве
. То, какой именно вариант получится, зависит от конкретной реализации алгоритма, но все варианты одинаково правильны. В то же время, в массиве ![c[]](../tex2png/cache/d9e2aa831637d909843d3ec6bd160813.png) никаких неоднозначностей быть не могло.
никаких неоднозначностей быть не могло.
Перейдём теперь к построению алгоритма. Входные данные:
char *s; // входная строка int n; // длина строки // константы const int maxlen = ...; // максимальная длина строки const int alphabet = 256; // размер алфавита, <= maxlen
На нулевой фазе мы должны отсортировать циклические подстроки длины  , т.е. отдельные символы строки, и разделить их на классы эквивалентности (просто одинаковые символы должны быть отнесены к одному классу эквивалентности). Это можно сделать тривиально, например, сортировкой подсчётом. Для каждого символа посчитаем, сколько раз он встретился. Потом по этой информации восстановим массив
, т.е. отдельные символы строки, и разделить их на классы эквивалентности (просто одинаковые символы должны быть отнесены к одному классу эквивалентности). Это можно сделать тривиально, например, сортировкой подсчётом. Для каждого символа посчитаем, сколько раз он встретился. Потом по этой информации восстановим массив ![p[]](../tex2png/cache/f41743bb1304c4dfaee1474862f9de80.png) . После этого, проходом по массиву
. После этого, проходом по массиву ![p[]](../tex2png/cache/f41743bb1304c4dfaee1474862f9de80.png) и сравнением символов, строится массив
и сравнением символов, строится массив ![c[]](../tex2png/cache/d9e2aa831637d909843d3ec6bd160813.png) .
.
int p[maxlen], cnt[maxlen], c[maxlen]; memset (cnt, 0, alphabet * sizeof(int)); for (int i=0; i<n; ++i) ++cnt[s[i]]; for (int i=1; i<alphabet; ++i) cnt[i] += cnt[i-1]; for (int i=0; i<n; ++i) p[--cnt[s[i]]] = i; c[p[0]] = 0; int classes = 1; for (int i=1; i<n; ++i) { if (s[p[i]] != s[p[i-1]]) ++classes; c[p[i]] = classes-1; }
Далее, пусть мы выполнили 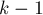 -ю фазу (т.е. вычислили значения массивов
-ю фазу (т.е. вычислили значения массивов ![p[]](../tex2png/cache/f41743bb1304c4dfaee1474862f9de80.png) и
и ![c[]](../tex2png/cache/d9e2aa831637d909843d3ec6bd160813.png) для неё), теперь научимся за
для неё), теперь научимся за  выполнять следующую,
выполнять следующую,  -ю, фазу. Поскольку фаз всего
-ю, фазу. Поскольку фаз всего 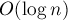 , это даст нам требуемый алгоритм с временем
, это даст нам требуемый алгоритм с временем 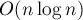 .
.
Для этого заметим, что циклическая подстрока длины 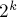 состоит из двух подстрок длины
состоит из двух подстрок длины 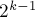 , которые мы можем сравнивать между собой за
, которые мы можем сравнивать между собой за  , используя информацию с предыдущей фазы — номера
, используя информацию с предыдущей фазы — номера ![c[]](../tex2png/cache/d9e2aa831637d909843d3ec6bd160813.png) классов эквивалентности. Таким образом, для подстроки длины
классов эквивалентности. Таким образом, для подстроки длины 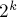 , начинающейся в позиции
, начинающейся в позиции  , вся необходимая информация содержится в паре чисел
, вся необходимая информация содержится в паре чисел ![(c[i], c[i+2^{k-1}])](../tex2png/cache/7d3622c6b869befe0a3e699e99cd3e0f.png) (повторимся, мы используем массив
(повторимся, мы используем массив ![c[]](../tex2png/cache/d9e2aa831637d909843d3ec6bd160813.png) с предыдущей фазы).
с предыдущей фазы).
![\ldots \overbrace{ \underbrace{ s_i \ldots s_{i+2[...]](../tex2png/cache/ae516e531e52b79fe882b86e620fd1b3.png)
Это даёт нам весьма простое решение: отсортировать подстроки длины 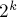 просто по этим парам чисел, это и даст нам требуемый порядок, т.е. массив
просто по этим парам чисел, это и даст нам требуемый порядок, т.е. массив ![p[]](../tex2png/cache/f41743bb1304c4dfaee1474862f9de80.png) . Однако обычная сортировка, выполняющаяся за время
. Однако обычная сортировка, выполняющаяся за время 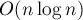 , нас не устроит — это даст алгоритм построения суффиксного массива с временем
, нас не устроит — это даст алгоритм построения суффиксного массива с временем 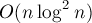 (зато этот алгоритм несколько проще в написании, чем описываемый ниже).
(зато этот алгоритм несколько проще в написании, чем описываемый ниже).
Как быстро выполнить такую сортировку пар? Поскольку элементы пар не превосходят  , то можно выполнить сортировку подсчётом. Однако для достижения лучшей скрытой в асимптотике константы вместо сортировки пар придём к сортировке просто чисел.
, то можно выполнить сортировку подсчётом. Однако для достижения лучшей скрытой в асимптотике константы вместо сортировки пар придём к сортировке просто чисел.
Воспользуемся здесь приёмом, на котором основана так называемая цифровая сортировка: чтобы отсортировать пары, отсортируем их сначала по вторым элементам, а затем — по первым элементам (но уже обязательно стабильной сортировкой, т.е. не нарушающей относительного порядка элементов при равенстве). Однако отдельно вторые элементы уже упорядочены — этот порядок задан в массиве ![p[]](../tex2png/cache/f41743bb1304c4dfaee1474862f9de80.png) от предыдущей фазы. Тогда, чтобы упорядочить пары по вторым элементам, надо просто от каждого элемента массива
от предыдущей фазы. Тогда, чтобы упорядочить пары по вторым элементам, надо просто от каждого элемента массива ![p[]](../tex2png/cache/f41743bb1304c4dfaee1474862f9de80.png) отнять
отнять 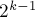 — это даст нам порядок сортировки пар по вторым элементам (ведь
— это даст нам порядок сортировки пар по вторым элементам (ведь ![p[]](../tex2png/cache/f41743bb1304c4dfaee1474862f9de80.png) даёт упорядочение подстрок длины
даёт упорядочение подстрок длины 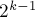 , и при переходе к строке вдвое большей длины эти подстроки становятся их вторыми половинками, поэтому от позиции второй половинки отнимается длина первой половинки).
, и при переходе к строке вдвое большей длины эти подстроки становятся их вторыми половинками, поэтому от позиции второй половинки отнимается длина первой половинки).
Таким образом, с помощью всего лишь вычитаний от элементов массива ![p[]](../tex2png/cache/f41743bb1304c4dfaee1474862f9de80.png) мы производим сортировку по вторым элементам пар. Теперь надо произвести стабильную сортировку по первым элементам пар, её уже можно выполнить за
мы производим сортировку по вторым элементам пар. Теперь надо произвести стабильную сортировку по первым элементам пар, её уже можно выполнить за  с помощью сортировки подсчётом.
с помощью сортировки подсчётом.
Осталось только пересчитать номера ![c[]](../tex2png/cache/d9e2aa831637d909843d3ec6bd160813.png) классов эквивалентности, но их уже легко получить, просто пройдя по полученной новой перестановке
классов эквивалентности, но их уже легко получить, просто пройдя по полученной новой перестановке ![p[]](../tex2png/cache/f41743bb1304c4dfaee1474862f9de80.png) и сравнивая соседние элементы (опять же, сравнивая как пары двух чисел).
и сравнивая соседние элементы (опять же, сравнивая как пары двух чисел).
Приведём реализацию выполнения всех фаз алгоритма, кроме нулевой. Вводятся дополнительно временные массивы 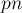 и
и 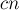 (
(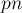 — содержит перестановку в порядке сортировки по вторым элементам пар,
— содержит перестановку в порядке сортировки по вторым элементам пар, 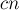 — новые номера классов эквивалентности).
— новые номера классов эквивалентности).
int pn[maxlen], cn[maxlen]; for (int h=0; (1<<h)<n; ++h) { for (int i=0; i<n; ++i) { pn[i] = p[i] - (1<<h); if (pn[i] < 0) pn[i] += n; } memset (cnt, 0, classes * sizeof(int)); for (int i=0; i<n; ++i) ++cnt[c[pn[i]]]; for (int i=1; i<classes; ++i) cnt[i] += cnt[i-1]; for (int i=n-1; i>=0; --i) p[--cnt[c[pn[i]]]] = pn[i]; cn[p[0]] = 0; classes = 1; for (int i=1; i<n; ++i) { int mid1 = (p[i] + (1<<h)) % n, mid2 = (p[i-1] + (1<<h)) % n; if (c[p[i]] != c[p[i-1]] || c[mid1] != c[mid2]) ++classes; cn[p[i]] = classes-1; } memcpy (c, cn, n * sizeof(int)); }
Этот алгоритм требует 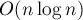 времени и
времени и  памяти. Впрочем, если учитывать ещё размер
памяти. Впрочем, если учитывать ещё размер  алфавита, то время работы становится
алфавита, то время работы становится 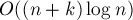 , а размер памяти —
, а размер памяти — 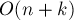 .
.
Применения
Нахождение наименьшего циклического сдвига строки
Вышеописанный алгоритм производит сортировку циклических сдвигов (если к строке не приписывать доллар), а потому ![p[0]](../tex2png/cache/13298d26b66ed695fab4fc3fc1f1dbd0.png) даст искомую позицию наименьшего циклического сдвига. Время работы —
даст искомую позицию наименьшего циклического сдвига. Время работы — 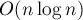 .
.
Поиск подстроки в строке
Пусть требуется в тексте 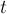 искать строку
искать строку  в режиме онлайн (т.е. заранее строку
в режиме онлайн (т.е. заранее строку  нужно считать неизвестной). Построим суффиксный массив для текста
нужно считать неизвестной). Построим суффиксный массив для текста 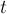 за
за 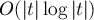 . Теперь подстроку
. Теперь подстроку  будем искать следующим образом: заметим, что искомое вхождение должно быть префиксом какого-либо суффикса
будем искать следующим образом: заметим, что искомое вхождение должно быть префиксом какого-либо суффикса 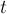 . Поскольку суффиксы у нас упорядочены (это даёт нам суффиксный массив), то подстроку
. Поскольку суффиксы у нас упорядочены (это даёт нам суффиксный массив), то подстроку  можно искать бинарным поиском по суффиксам строки. Сравнение текущего суффикса и подстроки
можно искать бинарным поиском по суффиксам строки. Сравнение текущего суффикса и подстроки  внутри бинарного поиска можно производить тривиально, за
внутри бинарного поиска можно производить тривиально, за 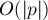 . Тогда асимптотика поиска подстроки в тексте становится
. Тогда асимптотика поиска подстроки в тексте становится 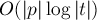 .
.
Сравнение двух подстрок строки
Требуется по заданной строке  , произведя некоторый её препроцессинг, научиться за
, произведя некоторый её препроцессинг, научиться за  отвечать на запросы сравнения двух произвольных подстрок (т.е. проверка, что первая подстрока равна/меньше/больше второй).
отвечать на запросы сравнения двух произвольных подстрок (т.е. проверка, что первая подстрока равна/меньше/больше второй).
Построим суффиксный массив за 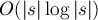 , при этом сохраним промежуточные результаты: нам понадобятся массивы
, при этом сохраним промежуточные результаты: нам понадобятся массивы ![c[]](../tex2png/cache/d9e2aa831637d909843d3ec6bd160813.png) от каждой фазы. Поэтому памяти потребуется тоже
от каждой фазы. Поэтому памяти потребуется тоже 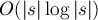 .
.
Используя эту информацию, мы можем за  сравнивать любые две подстроки длины, равной степени двойки: для этого достаточно сравнить номера классов эквивалентности из соответствующей фазы. Теперь надо обобщить этот способ на подстроки произвольной длины.
сравнивать любые две подстроки длины, равной степени двойки: для этого достаточно сравнить номера классов эквивалентности из соответствующей фазы. Теперь надо обобщить этот способ на подстроки произвольной длины.
Пусть теперь поступил очередной запрос сравнения двух подстрок длины 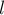 с началами в индексах
с началами в индексах  и
и  . Найдём наибольшую длину блока, помещающегося внутри подстроки такой длины, т.е. наибольшее
. Найдём наибольшую длину блока, помещающегося внутри подстроки такой длины, т.е. наибольшее  такое, что
такое, что 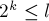 . Тогда сравнение двух подстрок можно заменить сравнением двух пар перекрывающихся блоков длины
. Тогда сравнение двух подстрок можно заменить сравнением двух пар перекрывающихся блоков длины 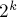 : сначала надо сравнить два блока, начинающихся в позициях
: сначала надо сравнить два блока, начинающихся в позициях  и
и  , а при равенстве — сравнить два блока, заканчивающихся в позициях
, а при равенстве — сравнить два блока, заканчивающихся в позициях 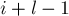 и
и 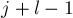 :
:
![\ldots \overbrace{ \underbrace{ s_i \ldots s_{i+l[...]](../tex2png/cache/a53b18ed921ac3f96534ea5531fcace9.png)
![\ldots \overbrace{ s_i \ldots \underbrace{ s_{i+l[...]](../tex2png/cache/a8c229d133c957aca2b6557f91de8f0a.png)
Таким образом, реализация получается примерно такой (здесь считается, что вызывающая процедура сама вычисляет  , поскольку сделать это за константное время не так легко (по-видимому, быстрее всего — предпосчётом), но в любом случае это не имеет отношения к применению суффиксного массива):
, поскольку сделать это за константное время не так легко (по-видимому, быстрее всего — предпосчётом), но в любом случае это не имеет отношения к применению суффиксного массива):
int compare (int i, int j, int l, int k) { pair<int,int> a = make_pair (c[k][i], c[k][i+l-(1<<k)]); pair<int,int> b = make_pair (c[k][j], c[k][j+l-(1<<k)]); return a == b ? 0 : a < b ? -1 : 1; }
Наибольший общий префикс двух подстрок: способ с дополнительной памятью
Требуется по заданной строке  , произведя некоторый её препроцессинг, научиться за
, произведя некоторый её препроцессинг, научиться за 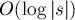 отвечать на запросы наибольшего общего префикса (longest common prefix, lcp) для двух произвольных суффиксов с позициями
отвечать на запросы наибольшего общего префикса (longest common prefix, lcp) для двух произвольных суффиксов с позициями  и
и  .
.
Способ, описываемый здесь, требует 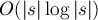 дополнительной памяти; другой способ, использующий линейный объём памяти, но неконстантное время ответа на запрос, описан в следующем разделе.
дополнительной памяти; другой способ, использующий линейный объём памяти, но неконстантное время ответа на запрос, описан в следующем разделе.
Построим суффиксный массив за 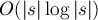 , при этом сохраним промежуточные результаты: нам понадобятся массивы
, при этом сохраним промежуточные результаты: нам понадобятся массивы ![c[]](../tex2png/cache/d9e2aa831637d909843d3ec6bd160813.png) от каждой фазы. Поэтому памяти потребуется тоже
от каждой фазы. Поэтому памяти потребуется тоже 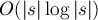 .
.
Пусть теперь поступил очередной запрос: пара индексов  и
и  . Воспользуемся тем, что мы можем за
. Воспользуемся тем, что мы можем за  сравнивать любые две подстроки длины, являющейся степенью двойки. Для этого будем перебирать степень двойки (от большей к меньшей), и для текущей степени проверять: если подстроки такой длины совпадают, то к ответу прибавить эту степень двойки, а наибольший общий префикс продолжим искать справа от одинаковой части, т.е. к
сравнивать любые две подстроки длины, являющейся степенью двойки. Для этого будем перебирать степень двойки (от большей к меньшей), и для текущей степени проверять: если подстроки такой длины совпадают, то к ответу прибавить эту степень двойки, а наибольший общий префикс продолжим искать справа от одинаковой части, т.е. к  и
и  надо прибавить текущую степень двойки.
надо прибавить текущую степень двойки.
Реализация:
int lcp (int i, int j) { int ans = 0; for (int k=log_n; k>=0; --k) if (c[k][i] == c[k][j]) { ans += 1<<k; i += 1<<k; j += 1<<k; } return ans; }
Здесь через 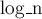 обозначена константа, равная логарифму
обозначена константа, равная логарифму  по основанию 2, округлённому вниз.
по основанию 2, округлённому вниз.
Наибольший общий префикс двух подстрок: способ без дополнительной памяти. Наибольший общий префикс двух соседних суффиксов
Требуется по заданной строке  , произведя некоторый её препроцессинг, научиться отвечать на запросы наибольшего общего префикса (longest common prefix, lcp) для двух произвольных суффиксов с позициями
, произведя некоторый её препроцессинг, научиться отвечать на запросы наибольшего общего префикса (longest common prefix, lcp) для двух произвольных суффиксов с позициями  и
и  .
.
В отличие от предыдущего метода, описываемый здесь будет выполнять препроцессинг строки за 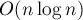 времени с
времени с  памяти. Результатом этого препроцессинга будет являться массив (который сам по себе является важным источником информации о строке, и потому использоваться для решения других задач). Ответы же на запрос будут производиться как результат выполнения запроса RMQ (минимум на отрезке, range minimum query) в этом массиве, поэтому при разных реализациях можно получить как логарифмическое, так и константное времена работы.
памяти. Результатом этого препроцессинга будет являться массив (который сам по себе является важным источником информации о строке, и потому использоваться для решения других задач). Ответы же на запрос будут производиться как результат выполнения запроса RMQ (минимум на отрезке, range minimum query) в этом массиве, поэтому при разных реализациях можно получить как логарифмическое, так и константное времена работы.
Базой для этого алгоритма является следующая идея: найдём каким-нибудь образом наибольшие общие префиксы для каждой соседней в порядке сортировки пары суффиксов. Иными словами, построим массив ![{\rm lcp}[0 \ldots n-2]](../tex2png/cache/7ccb12a81f3611ba7af3f10d0ab280e7.png) , где
, где ![{\rm lcp}[i]](../tex2png/cache/9ef59b64bf22fbd516bcf192980782d8.png) равен наибольшему общему префиксу суффиксов
равен наибольшему общему префиксу суффиксов ![p[i]](../tex2png/cache/6fa33a48f7fff7f52d08a07ab012145a.png) и
и ![p[i+1]](../tex2png/cache/d006fba63190eb9a53a092d42694a3da.png) . Этот массив даст нам ответ для любых двух соседних суффиксов строки. Тогда ответ для любых двух суффиксов, не обязательно соседних, можно получить по этому массиву. В самом деле, пусть поступил запрос с некоторыми номерами суффиксов
. Этот массив даст нам ответ для любых двух соседних суффиксов строки. Тогда ответ для любых двух суффиксов, не обязательно соседних, можно получить по этому массиву. В самом деле, пусть поступил запрос с некоторыми номерами суффиксов  и
и  . Найдём эти индексы в суффиксном массиве, т.е. пусть
. Найдём эти индексы в суффиксном массиве, т.е. пусть 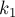 и
и 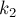 — их позиции в массиве
— их позиции в массиве ![p[]](../tex2png/cache/f41743bb1304c4dfaee1474862f9de80.png) (упорядочим их, т.е. пусть
(упорядочим их, т.е. пусть 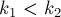 ). Тогда ответом на данный запрос будет минимум в массиве
). Тогда ответом на данный запрос будет минимум в массиве 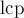 , взятый на отрезке
, взятый на отрезке ![[k_1; k_2-1]](../tex2png/cache/53c0b0104384de40187b428af79df862.png) . В самом деле, переход от суффикса
. В самом деле, переход от суффикса  к суффиксу
к суффиксу  можно заменить целой цепочкой переходов, начинающейся с суффикса
можно заменить целой цепочкой переходов, начинающейся с суффикса  и заканчивающейся в суффиксе
и заканчивающейся в суффиксе  , но включающей в себя все промежуточные суффиксы, находящиеся в порядке сортировки между ними.
, но включающей в себя все промежуточные суффиксы, находящиеся в порядке сортировки между ними.
Таким образом, если мы имеем такой массив 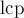 , то ответ на любой запрос наибольшего общего префикса сводится к запросу минимума на отрезке массива
, то ответ на любой запрос наибольшего общего префикса сводится к запросу минимума на отрезке массива 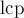 . Эта классическая задача минимума на отрезке (range minimum query, RMQ) имеет множество решений с различными асимптотиками, описанные здесь.
. Эта классическая задача минимума на отрезке (range minimum query, RMQ) имеет множество решений с различными асимптотиками, описанные здесь.
Итак, основная наша задача — построение этого массива 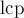 . Строить его мы будем по ходу алгоритма построения суффиксного массива: на каждой текущей итерации будем строить массив
. Строить его мы будем по ходу алгоритма построения суффиксного массива: на каждой текущей итерации будем строить массив 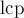 для циклических подстрок текущей длины.
для циклических подстрок текущей длины.
После нулевой итерации массив 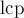 , очевидно, должен быть нулевым.
, очевидно, должен быть нулевым.
Пусть теперь мы выполнили 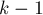 -ю итерацию, получили от неё массив
-ю итерацию, получили от неё массив 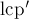 , и должны на текущей
, и должны на текущей  -й итерации пересчитать этот массив, получив новое его значение
-й итерации пересчитать этот массив, получив новое его значение 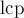 . Как мы помним, в алгоритме построения суффиксного массива циклические подстроки длины
. Как мы помним, в алгоритме построения суффиксного массива циклические подстроки длины 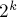 разбивались пополам на две подстроки длины
разбивались пополам на две подстроки длины 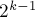 ; воспользуемся этим же приёмом и для построения массива
; воспользуемся этим же приёмом и для построения массива 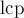 .
.
Итак, пусть на текущей итерации алгоритм вычисления суффиксного массива выполнил свою работу, нашёл новое значение перестановки ![p[]](../tex2png/cache/f41743bb1304c4dfaee1474862f9de80.png) подстрок. Будем теперь идти по этому массиву и смотреть пары соседних подстрок:
подстрок. Будем теперь идти по этому массиву и смотреть пары соседних подстрок: ![p[i]](../tex2png/cache/6fa33a48f7fff7f52d08a07ab012145a.png) и
и ![p[i+1]](../tex2png/cache/d006fba63190eb9a53a092d42694a3da.png) ,
, 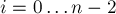 . Разбивая каждую подстроку пополам, мы получаем две различных ситуации: 1) первые половинки подстрок в позициях
. Разбивая каждую подстроку пополам, мы получаем две различных ситуации: 1) первые половинки подстрок в позициях ![p[i]](../tex2png/cache/6fa33a48f7fff7f52d08a07ab012145a.png) и
и ![p[i+1]](../tex2png/cache/d006fba63190eb9a53a092d42694a3da.png) различаются, и 2) первые половинки совпадают (напомним, такое сравнение можно легко производить, просто сравнивая номера классов
различаются, и 2) первые половинки совпадают (напомним, такое сравнение можно легко производить, просто сравнивая номера классов ![c[]](../tex2png/cache/d9e2aa831637d909843d3ec6bd160813.png) с предыдущей итерации). Рассмотрим каждый из этих случаев отдельно.
с предыдущей итерации). Рассмотрим каждый из этих случаев отдельно.
1) Первые половинки подстрок различались. Заметим, что тогда на предыдущем шаге эти первые половинки необходимо были соседними. В самом деле, классы эквивалентности не могли исчезать (а могут только появляться), поэтому все различные подстроки длины 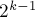 дадут (в качестве первых половинок) на текущей итерации различные подстроки длины
дадут (в качестве первых половинок) на текущей итерации различные подстроки длины 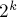 , и в том же порядке. Таким образом, для определения
, и в том же порядке. Таким образом, для определения ![{\rm lcp}[i]](../tex2png/cache/9ef59b64bf22fbd516bcf192980782d8.png) в этом случае надо просто взять соответствующее значение из массива
в этом случае надо просто взять соответствующее значение из массива 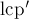 .
.
2) Первые половинки совпадали. Тогда вторые половинки могли как совпадать, так и различаться; при этом, если они различаются, то они совсем не обязательно должны были быть соседними на предыдущей итерации. Поэтому в этом случае нет простого способа определить ![{\rm lcp}[i]](../tex2png/cache/9ef59b64bf22fbd516bcf192980782d8.png) . Для его определения надо поступить так же, как мы и собираемся потом вычислять наибольший общий префикс для любых двух суффиксов: надо выполнить запрос минимума (RMQ) на соответствующем отрезке массива
. Для его определения надо поступить так же, как мы и собираемся потом вычислять наибольший общий префикс для любых двух суффиксов: надо выполнить запрос минимума (RMQ) на соответствующем отрезке массива 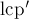 .
.
Оценим асимптотику такого алгоритма. Как мы видели при разборе этих двух случаев, только второй случай даёт увеличение числа классов эквивалентности. Иными словами, можно говорить о том, что каждый новый класс эквивалентности появляется вместе с одним запросом RMQ. Поскольку всего классов эквивалентности может быть до  , то и искать минимум мы должны за асимптотику
, то и искать минимум мы должны за асимптотику 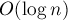 . А для этого надо использовать уже какую-то структуру данных для минимума на отрезке; эту структуру данных надо будет строить заново на каждой итерации (которых всего
. А для этого надо использовать уже какую-то структуру данных для минимума на отрезке; эту структуру данных надо будет строить заново на каждой итерации (которых всего 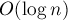 ). Хорошим вариантом структуры данных будет Дерево отрезков: его можно построить за
). Хорошим вариантом структуры данных будет Дерево отрезков: его можно построить за  , а потом выполнять запросы за
, а потом выполнять запросы за 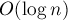 , что как раз и даёт нам итоговую асимптотику
, что как раз и даёт нам итоговую асимптотику 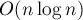 .
.
Реализация:
int lcp[maxlen], lcpn[maxlen], lpos[maxlen], rpos[maxlen]; memset (lcp, 0, sizeof lcp); for (int h=0; (1<<h)<n; ++h) { for (int i=0; i<n; ++i) rpos[c[p[i]]] = i; for (int i=n-1; i>=0; --i) lpos[c[p[i]]] = i; ... все действия по построению суфф. массива, кроме последней строки (memcpy) ... rmq_build (lcp, n-1); for (int i=0; i<n-1; ++i) { int a = p[i], b = p[i+1]; if (c[a] != c[b]) lcpn[i] = lcp[rpos[c[a]]]; else { int aa = (a + (1<<h)) % n, bb = (b + (1<<h)) % n; lcpn[i] = (1<<h) + rmq (lpos[c[aa]], rpos[c[bb]]-1); lcpn[i] = min (n, lcpn[i]); } } memcpy (lcp, lcpn, (n-1) * sizeof(int)); memcpy (c, cn, n * sizeof(int)); }
Здесь помимо массива ![\rm lcp[]](../tex2png/cache/a5d07488021f4ad569b61e022ef927ad.png) вводится временный массив
вводится временный массив ![\rm lcpn[]](../tex2png/cache/ec5026a642d21abf60f08f9b8abad120.png) с его новым значением. Также поддерживается массив
с его новым значением. Также поддерживается массив ![\rm pos[]](../tex2png/cache/86dc3261b0399ac6cb9fa5bb406dd403.png) , который для каждой подстроки хранит её позицию в перестановке
, который для каждой подстроки хранит её позицию в перестановке ![p[]](../tex2png/cache/f41743bb1304c4dfaee1474862f9de80.png) . Функция
. Функция 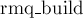 — некоторая функция, строящая структуру данных для минимума по массиву-первому аргументу, размер его передаётся вторым аргументом. Функция
— некоторая функция, строящая структуру данных для минимума по массиву-первому аргументу, размер его передаётся вторым аргументом. Функция 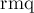 возвращает минимум на отрезке: с первого аргумента по второй включительно.
возвращает минимум на отрезке: с первого аргумента по второй включительно.
Из самого алгоритма построения суффиксного массива пришлось только вынести копирование массива ![c[]](../tex2png/cache/d9e2aa831637d909843d3ec6bd160813.png) , поскольку во время вычисления
, поскольку во время вычисления 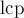 нам понадобятся старые значения этого массива.
нам понадобятся старые значения этого массива.
Стоит отметить, что наша реализация находит длину общего префикса для циклических подстрок, в то время как на практике чаще бывает нужной длина общего префикса для суффиксов в их обычном понимании. В этом случае надо просто ограничить значения 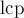 по окончании работы алгоритма:
по окончании работы алгоритма:
for (int i=0; i<n-1; ++i) lcp[i] = min (lcp[i], min (n-p[i], n-p[i+1]));
Для любых двух суффиксов длину их наибольшего общего префикса теперь можно найти как минимум на соответствующем отрезке массива 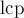 :
:
for (int i=0; i<n; ++i) pos[p[i]] = i; rmq_build (lcp, n-1); ... поступил запрос (i,j) на нахождение LCP ... int result = rmq (min(i,j), max(i,j)-1);
Количество различных подстрок
Выполним препроцессинг, описанный в предыдущем разделе: за 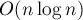 времени и
времени и  памяти мы для каждой пары соседних в порядке сортировки суффиксов найдём длину их наибольшего общего префикса. Найдём теперь по этой информации количество различных подстрок в строке.
памяти мы для каждой пары соседних в порядке сортировки суффиксов найдём длину их наибольшего общего префикса. Найдём теперь по этой информации количество различных подстрок в строке.
Для этого будем рассматривать, какие новые подстроки начинаются в позиции ![p[0]](../tex2png/cache/13298d26b66ed695fab4fc3fc1f1dbd0.png) , затем в позиции
, затем в позиции ![p[1]](../tex2png/cache/973461b3241ee0607c4ce84e4169e8a6.png) , и т.д. Фактически, мы берём очередной в порядке сортировки суффикс и смотрим, какие его префиксы дают новые подстроки. Тем самым мы, очевидно, не упустим из виду никакие из подстрок.
, и т.д. Фактически, мы берём очередной в порядке сортировки суффикс и смотрим, какие его префиксы дают новые подстроки. Тем самым мы, очевидно, не упустим из виду никакие из подстрок.
Пользуясь тем, что суффиксы у нас уже отсортированы, нетрудно понять, что текущий суффикс ![p[i]](../tex2png/cache/6fa33a48f7fff7f52d08a07ab012145a.png) даст в качестве новых подстрок все свои префиксы, кроме совпадающих с префиксами суффикса
даст в качестве новых подстрок все свои префиксы, кроме совпадающих с префиксами суффикса ![p[i-1]](../tex2png/cache/e9d4e351799f1afc17a73678f1e782c3.png) . Т.е. все его префиксы, кроме
. Т.е. все его префиксы, кроме ![{\rm lcp}[i-1]](../tex2png/cache/b9b25cbc6351d371a02a6b28ecaa8ca2.png) первых, дадут новые подстроки. Поскольку длина текущего суффикса равна
первых, дадут новые подстроки. Поскольку длина текущего суффикса равна ![n-p[i]](../tex2png/cache/233424f2a1d720f3b1c1e4f3009281f3.png) , то окончательно получаем, что текущий суффикс
, то окончательно получаем, что текущий суффикс ![p[i]](../tex2png/cache/6fa33a48f7fff7f52d08a07ab012145a.png) даёт
даёт ![n-p[i]-{\rm lcp}[i-1]](../tex2png/cache/1bd3f25b5a810eb12eea587e0bf48ef1.png) новых подстрок. Суммируя это по всем суффиксам (для самого первого,
новых подстрок. Суммируя это по всем суффиксам (для самого первого, ![p[0]](../tex2png/cache/13298d26b66ed695fab4fc3fc1f1dbd0.png) , отнимать нечего — прибавится просто
, отнимать нечего — прибавится просто ![n-p[0]](../tex2png/cache/85fb853fc040180ff638a42820bc838a.png) ), получаем ответ на задачу:
), получаем ответ на задачу:
![\sum_{i=0}^n (n - p[i]) - \sum_{i=0}^{n-1} {\rm l[...]](../tex2png/cache/97acc8c31d5aa1d426f281e3d94ffddb.png)
Задачи в online judges
Задачи, которые можно решить, используя суффиксный массив: