Интегрирование по формуле Симпсона

Требуется посчитать значение определённого интеграла:

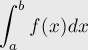
$\int_a^b f(x) dx$

Решение, описываемое здесь, было опубликовано в одной из диссертаций Томаса Симпсона (Thomas Simpson) в 1743 г.

Формула Симпсона

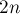Пусть $n$ — некоторое натуральное число. Разобьём отрезок интегрирования $[a;b]$ на $2n$ равных частей:

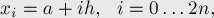
$x_i = a + i h,~~i = 0 \ldots 2n,$
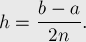
$h = \frac{ b-a }{ 2n }.$

Теперь посчитаем интеграл отдельно на каждом из отрезков $[x_{2i-2}, x_{2i}], i = 1 \ldots n$ , а затем сложим все значения.

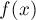Итак, пусть мы рассматриваем очередной отрезок $[x_{2i-2}, x_{2i}], i = 1 \ldots n$ . Заменим функцию $f(x)$ на нём параболой, проходящей через 3 точки 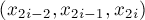$(x_{2i-2},x_{2i-1},x_{2i})$ . Такая парабола всегда существует и единственна. Её можно найти аналитически, затем останется только проинтегрировать выражение для неё, и окончательно получаем:

$\int_{x_{2i-2}}^{x_{2i}} f(x) dx = \left( f(x_{2i[...]$

Складывая эти значения по всем отрезкам, получаем окончательную формулу Симпсона:

$\int_a^b f(x) dx = \left( f(x_0) + 4 f(x_1) + 2 f[...]$

Погрешность

Погрешность, даваемая формулой Симпсона, не превосходит по модулю величины:

$\frac{ 1 }{ 180 } h^4 (b - a) \max_{a \le x \le b[...]$

Таким образом, погрешность имеет порядок уменьшения как 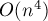$O (n^4)$ .

Реализация

Здесь 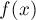$f(x)$ — некоторая пользовательская функция.

double a, b; // входные данные
const int N = 1000*1000; // количество шагов (уже умноженное на 2)
double s = 0;
double h = (b - a) / N;
for (int i=0; i<=N; ++i) {
	double x = a + h * i;
	s += f(x) * ((i==0 || i==N) ? 1 : ((i&1)==0) ? 2 : 4);
}
s *= h / 3;