MAXimal
добавлено: 9 Sep 2008 19:28
редактировано: 20 Sep 2010 18:45
Содержание [скрыть]
Вычисление факториала по модулю
В некоторых случаях необходимо считать по некоторому простому модулю  сложные формулы, которые в том числе могут содержать факториалы. Здесь мы рассмотрим случай, когда модуль
сложные формулы, которые в том числе могут содержать факториалы. Здесь мы рассмотрим случай, когда модуль  сравнительно мал. Понятно, что эта задача имеет смысл только в том случае, когда факториалы входят и в числитель, и в знаменатель дробей. Действительно, факториал
сравнительно мал. Понятно, что эта задача имеет смысл только в том случае, когда факториалы входят и в числитель, и в знаменатель дробей. Действительно, факториал 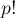 и все последующие обращаются в ноль по модулю
и все последующие обращаются в ноль по модулю  , однако в дробях все множители, содержащие
, однако в дробях все множители, содержащие  , могут сократиться, и полученное выражение уже будет отлично от нуля по модулю
, могут сократиться, и полученное выражение уже будет отлично от нуля по модулю  .
.
Таким образом, формально задача такая. Требуется вычислить 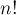 по простому модулю
по простому модулю  , при этом не учитывая все кратные
, при этом не учитывая все кратные  множители, входящие в факториал. Научившись эффективно вычислять такой факториал, мы сможем быстро вычислять значение различных комбинаторных формул (например, Биномиальные коэффициенты).
множители, входящие в факториал. Научившись эффективно вычислять такой факториал, мы сможем быстро вычислять значение различных комбинаторных формул (например, Биномиальные коэффициенты).
Алгоритм
Выпишем этот "модифицированный" факториал в явном виде:
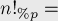
![= 1 \cdot 2 \cdot 3 \cdot \ldots \cdot (p-2) \cdo[...]](../tex2png/cache/296b123a78bc168a7d7fab6aa98fd927.png)
![\cdot (p^2-1) \cdot \underbrace{1}_{p^2} \cdot (p[...]](../tex2png/cache/774a047bc2ce29c9c6f429b93e290015.png)
![= 1 \cdot 2 \cdot 3 \cdot \ldots \cdot (p-2) \cdo[...]](../tex2png/cache/0bcaed0449badc1e040fb3a9a96a16c9.png)
![\cdot 1 \cdot 2 \cdot \ldots \cdot (n\%p) \pmod p[...]](../tex2png/cache/7fa91feca02eac37349529244026ce6f.png)
При такой записи видно, что "модифицированный" факториал распадается на несколько блоков длины  (последний блок, возможно, короче), которые все одинаковы, за исключением последнего элемента:
(последний блок, возможно, короче), которые все одинаковы, за исключением последнего элемента:
![n!_{\%p} = \underbrace{ 1 \cdot 2 \cdot \ldots \c[...]](../tex2png/cache/5685c685028e80cd7e723828c12d3880.png)
![\cdot \underbrace{ 1 \cdot 2 \cdot \ldots \cdot ([...]](../tex2png/cache/680c978b44708b069e29ac18ea587ef6.png)
Общую часть блоков посчитать легко — это просто 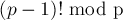 , которую можно посчитать программно или по теореме Вильсона (Wilson) сразу найти
, которую можно посчитать программно или по теореме Вильсона (Wilson) сразу найти 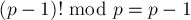 . Чтобы перемножить эти общие части всех блоков, надо найденную величину возвести в степень по модулю
. Чтобы перемножить эти общие части всех блоков, надо найденную величину возвести в степень по модулю  , что можно сделать за
, что можно сделать за 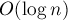 операций (см. Бинарное возведение в степень; впрочем, можно заметить, что мы фактически возводим минус единицу в какую-то степень, а потому результатом всегда будет либо
операций (см. Бинарное возведение в степень; впрочем, можно заметить, что мы фактически возводим минус единицу в какую-то степень, а потому результатом всегда будет либо  , либо
, либо 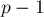 , в зависимости от чётности показателя. Значение в последнем, неполном блоке тоже можно посчитать отдельно за
, в зависимости от чётности показателя. Значение в последнем, неполном блоке тоже можно посчитать отдельно за 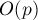 . Остались только последние элементы блоков, рассмотрим их внимательнее:
. Остались только последние элементы блоков, рассмотрим их внимательнее:
![n!_{\%p} = \underbrace{ \ldots \cdot 1 } \cdot \u[...]](../tex2png/cache/b8295392eb63e0e0d26d5feee3608151.png)
И мы снова пришли к "модифицированному" факториалу, но уже меньшей размерности (столько, сколько было полных блоков, а их было 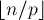 ). Таким образом, вычисление "модифицированного" факториала
). Таким образом, вычисление "модифицированного" факториала 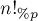 мы свели за
мы свели за 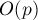 операций к вычислению уже
операций к вычислению уже 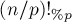 . Раскрывая эту рекуррентную зависимость, мы получаем, что глубина рекурсии будет
. Раскрывая эту рекуррентную зависимость, мы получаем, что глубина рекурсии будет 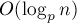 , итого асимптотика алгоритма получается
, итого асимптотика алгоритма получается 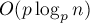 .
.
Реализация
Понятно, что при реализации не обязательно использовать рекурсию в явном виде: поскольку рекурсия хвостовая, её легко развернуть в цикл.
int factmod (int n, int p) { int res = 1; while (n > 1) { res = (res * ((n/p) % 2 ? p-1 : 1)) % p; for (int i=2; i<=n%p; ++i) res = (res * i) % p; n /= p; } return res % p; }
Эта реализация работает за 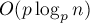 .
.