Точка пересечения прямых

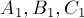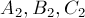Пусть нам даны две прямые, заданные своими коэффициентами $A_1, B_1, C_1$ и $A_2, B_2, C_2$ . Требуется найти их точку пересечения, или выяснить, что прямые параллельны.

Решение

Если две прямые не параллельны, то они пересекаются. Чтобы найти точку пересечения, достаточно составить из двух уравнений прямых систему и решить её:

$\cases{ A_1 x + B_1 y + C_1 = 0, \cr A_2 x + B_2[...]$

Пользуясь формулой Крамера, сразу находим решение системы, которое и будет искомой точкой пересечения:

$x = - \frac{ \left|\matrix{C_1&B_1 \cr C_2&B_2}\r[...]$
$y = - \frac{ \left|\matrix{A_1&C_1 \cr A_2&C_2}\r[...]$

Если знаменатель нулевой, т.е.

$\left|\matrix{A_1&B_1 \cr A_2&B_2}\right| = A_1 B[...]$

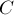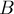то система решений не имеет (прямые параллельны и не совпадают) или имеет бесконечно много (прямые совпадают). Если необходимо различить эти два случая, надо проверить, что коэффициенты $C$ прямых пропорциональны с тем же коэффициентом пропорциональности, что и коэффициенты $A$ и $B$ , для чего достаточно посчитать два определителя, если они оба равны нулю, то прямые совпадают:

$\left|\matrix{ A_1 & C_1 \cr A_2 & C_2 }\right|, [...]$

Реализация

struct pt {
	double x, y;
};
 
struct line {
	double a, b, c;
};
 
const double EPS = 1e-9;
 
double det (double a, double b, double c, double d) {
	return a * d - b * c;
}
 
bool intersect (line m, line n, pt & res) {
	double zn = det (m.a, m.b, n.a, n.b);
	if (abs (zn) < EPS)
		return false;
	res.x = - det (m.c, m.b, n.c, n.b) / zn;
	res.y = - det (m.a, m.c, n.a, n.c) / zn;
	return true;
}
 
bool parallel (line m, line n) {
	return abs (det (m.a, m.b, n.a, n.b)) < EPS;
}
 
bool equivalent (line m, line n) {
	return abs (det (m.a, m.b, n.a, n.b)) < EPS
		&& abs (det (m.a, m.c, n.a, n.c)) < EPS
		&& abs (det (m.b, m.c, n.b, n.c)) < EPS;
}