Поиск пары пересекающихся отрезков алгоритмом заметающей прямой за O (N log N)

Даны $n$ отрезков на плоскости. Требуется проверить, пересекаются ли друг с другом хотя бы два из них. (Если ответ положителен — то вывести эту пару пересекающихся отрезков; среди нескольких ответов достаточно выбрать любой из них.)

Наивный алгоритм решения — перебрать за 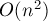$O (n^2)$ все пары отрезков и проверить для каждой пары, пересекаются они или нет. В данной статье описывается алгоритм с временем работы 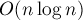$O (n \log n)$ , который основан на принципе сканирующей (заметающей) прямой (по-английски: "sweep line").

Алгоритм

Проведём мысленно вертикальную прямую 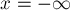$x = -\infty$ и начнём двигать эту прямую вправо. По ходу своего движения эта прямая будет встречаться с отрезками, причём в любой момент времени каждый отрезок будет пересекаться с нашей прямой по одной точке (мы пока будем считать, что вертикальных отрезков нет).

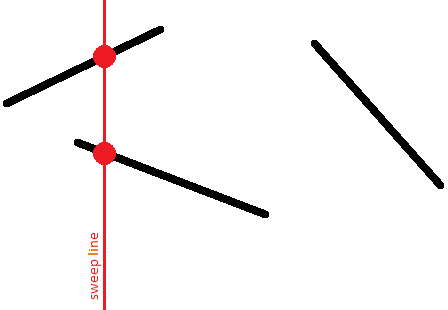
Таким образом, для каждого отрезка в какой-то момент времени его точка появится на сканирующей прямой, затем с движением прямой будет двигаться и эта точка, и, наконец, в какой-то момент отрезок исчезнет с прямой.

Нас интересует относительный порядок отрезков по вертикали. А именно, мы будем хранить список отрезков, пересекающих сканирующую прямую в данный момент времени, где отрезки будут отсортированы по их $y$ -координате на сканирующей прямой.

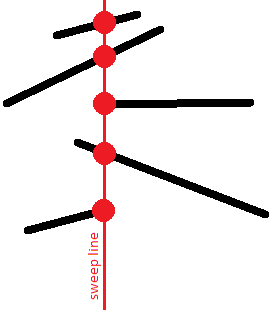
Этот порядок интересен тем, что пересекающиеся отрезки будут иметь одинаковую $y$ -координату хотя бы в один момент времени:

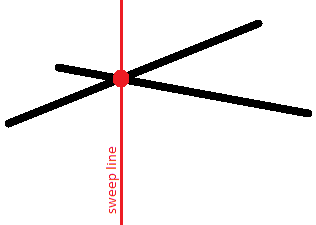
Сформулируем ключевые утверждения:

Для поиска пересекающейся пары достаточно рассматривать при каждом фиксированном положении сканирующей прямой только соседние отрезки.
Достаточно рассматривать сканирующую прямую не во всех возможных действительных позициях 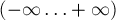$(-\infty \ldots +\infty)$ , а только в тех позициях, когда появляются новые отрезки или исчезают старые. Иными словами, достаточно ограничиться лишь только положениями, равными абсциссам точек-концов отрезков.
При появлении нового отрезка достаточно вставить его в нужное место в список, полученный для предыдущей сканирующей прямой. Проверять на пересечение надо только добавляемый отрезок с его непосредственными соседями в списке сверху и снизу.
При исчезновении отрезка достаточно удалить его из текущего списка. После этого надо проверить на пересечение с верхним и нижним соседями в списке.
Других изменений в порядке следования отрезков в списке, кроме описанных, не существует. Других проверок на пересечения производить не надо.

Для понимания истинности этих утверждений достаточно следующих замечаний:

Два непересекающихся отрезка никогда не меняют своего относительного порядка.
В самом деле, если один отрезок сначала был выше другого, а затем стал ниже, то между двумя этими моментами произошло пересечение этих двух отрезков.
Иметь совпадающие $y$ -координаты два непересекающихся отрезка также не могут.
Из этого следует, что в момент появления отрезка мы можем найти в очереди позицию для этого отрезка, и больше этот отрезок переставлять в очереди не придётся: его порядок относительно других отрезков в очереди меняться не будет.
Два пересекающихся отрезка в момент точки своего пересечения окажутся соседями друг друга в очереди.
Следовательно, для нахождения пары пересекающихся отрезков достаточно проверить на пересечение только все те пары отрезков, которые когда-нибудь за время движения сканирующей прямой хотя бы раз были соседями друг друга.
Легко заметить, что этого достаточно лишь проверять добавляемый отрезок со своими верхним и нижним соседями, а также при удалении отрезка — его верхнего и нижнего соседей (которые после удаления станут соседями друг друга).
Следует обратить внимание, что при фиксированном положении сканирующей прямой мы сначала должны произвести добавление всех появляющихся здесь отрезков, и лишь затем — удаление всех исчезающих здесь отрезков.
Тем самым, мы не пропустим пересечения отрезков по вершине: т.е. такие случаи, когда два отрезка имеют общую вершину.
Заметим, что вертикальные отрезки на самом деле никак не влияют на корректность алгоритма.
Эти отрезки выделяются тем, что они появляются и исчезают в один и тот же момент времени. Однако, за счёт предыдущего замечания, мы знаем, что сначала все отрезки будут добавлены в очередь, и лишь затем будут удалены. Следовательно, если вертикальный отрезок пересекается с каким-то другим открытым в этот момент отрезком (в том числе вертикальным), то это будет обнаружено.
В какое место очереди помещать вертикальные отрезки? Ведь вертикальный отрезок не имеет одной определённой $y$ -координаты, он простирается на целый отрезок по $y$ -координате. Однако легко понять, что в качестве $y$ -координаты можно взять любую координату из этого отрезка.

Таким образом, весь алгоритм совершит не более 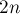$2n$ тестов на пересечение пары отрезков, и совершит 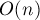$O (n)$ операций с очередью отрезков (по $O(1)$ операций в моменты появления и исчезновения каждого отрезка).

Итоговая асимптотика алгоритма составляет, таким образом, 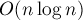$O (n \log n)$ .

Реализация

Приведём полную реализацию описанного алгоритма:

const double EPS = 1E-9;
 
struct pt {
	double x, y;
};
 
struct seg {
	pt p, q;
	int id;
 
	double get_y (double x) const {
		if (abs (p.x - q.x) < EPS)  return p.y;
		return p.y + (q.y - p.y) * (x - p.x) / (q.x - p.x);
	}
};
 
 
inline bool intersect1d (double l1, double r1, double l2, double r2) {
	if (l1 > r1)  swap (l1, r1);
	if (l2 > r2)  swap (l2, r2);
	return max (l1, l2) <= min (r1, r2) + EPS;
}
 
inline int vec (const pt & a, const pt & b, const pt & c) {
	double s = (b.x - a.x) * (c.y - a.y) - (b.y - a.y) * (c.x - a.x);
	return abs(s)<EPS ? 0 : s>0 ? +1 : -1;
}
 
bool intersect (const seg & a, const seg & b) {
	return intersect1d (a.p.x, a.q.x, b.p.x, b.q.x)
		&& intersect1d (a.p.y, a.q.y, b.p.y, b.q.y)
		&& vec (a.p, a.q, b.p) * vec (a.p, a.q, b.q) <= 0
		&& vec (b.p, b.q, a.p) * vec (b.p, b.q, a.q) <= 0;
}
 
 
bool operator< (const seg & a, const seg & b) {
	double x = max (min (a.p.x, a.q.x), min (b.p.x, b.q.x));
	return a.get_y(x) < b.get_y(x) - EPS;
}
 
 
struct event {
	double x;
	int tp, id;
 
	event() { }
	event (double x, int tp, int id)
		: x(x), tp(tp), id(id)
	{ }
 
	bool operator< (const event & e) const {
		if (abs (x - e.x) > EPS)  return x < e.x;
		return tp > e.tp;
	}
};
 
set<seg> s;
vector < set<seg>::iterator > where;
 
inline set<seg>::iterator prev (set<seg>::iterator it) {
	return it == s.begin() ? s.end() : --it;
}
 
inline set<seg>::iterator next (set<seg>::iterator it) {
	return ++it;
}
 
pair<int,int> solve (const vector<seg> & a) {
	int n = (int) a.size();
	vector<event> e;
	for (int i=0; i<n; ++i) {
		e.push_back (event (min (a[i].p.x, a[i].q.x), +1, i));
		e.push_back (event (max (a[i].p.x, a[i].q.x), -1, i));
	}
	sort (e.begin(), e.end());
 
	s.clear();
	where.resize (a.size());
	for (size_t i=0; i<e.size(); ++i) {
		int id = e[i].id;
		if (e[i].tp == +1) {
			set<seg>::iterator
				nxt = s.lower_bound (a[id]),
				prv = prev (nxt);
			if (nxt != s.end() && intersect (*nxt, a[id]))
				return make_pair (nxt->id, id);
			if (prv != s.end() && intersect (*prv, a[id]))
				return make_pair (prv->id, id);
			where[id] = s.insert (nxt, a[id]);
		}
		else {
			set<seg>::iterator
				nxt = next (where[id]),
				prv = prev (where[id]);
			if (nxt != s.end() && prv != s.end() && intersect (*nxt, *prv))
				return make_pair (prv->id, nxt->id);
			s.erase (where[id]);
		}
	}
 
	return make_pair (-1, -1);
}

Основная функция здесь — 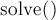$\rm solve()$ , которая возвращает номера найденных пересекающихся отрезков, либо 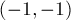$(-1, -1)$ , если пересечения отсутствуют.

Проверка на пересечение двух отрезков осуществляется функцией 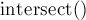$\rm intersect()$ , с помощью алгоритма на основе ориентированной площади треугольника.

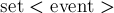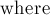Очередь отрезков в глобальной переменной $s$ — $\rm set<event>$ . Итераторы, указывающие положение каждого отрезка в очереди (для удобного удаления отрезков из очереди), хранятся в глобальном массиве $\rm where$ .

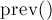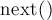Введены также две вспомогательные функции $\rm prev()$ и $\rm next()$ , которые возвращают итераторы на предыдущий и следующий элементы (либо 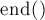$\rm end()$ , если такового не существует).

Константа 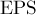$\rm EPS$ обозначает погрешность сравнения двух вещественных чисел (в основном она используется при проверке двух отрезков на пересечение).