добавлено: 10 Jun 2008 17:58
редактировано: 17 Oct 2012 14:55
Расширенный алгоритм Евклида
В то время как "обычный" алгоритм Евклида просто находит наибольший общий делитель двух чисел  и
и  , расширенный алгоритм Евклида находит помимо НОД также коэффициенты
, расширенный алгоритм Евклида находит помимо НОД также коэффициенты  и
и  такие, что:
такие, что:
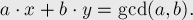
Т.е. он находит коэффициенты, с помощью которых НОД двух чисел выражается через сами эти числа.
Алгоритм
Внести вычисление этих коэффициентов в алгоритм Евклида несложно, достаточно вывести формулы, по которым они меняются при переходе от пары 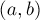 к паре
к паре 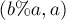 (знаком процента мы обозначаем взятие остатка от деления).
(знаком процента мы обозначаем взятие остатка от деления).
Итак, пусть мы нашли решение 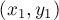 задачи для новой пары
задачи для новой пары 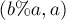 :
:
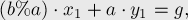
и хотим получить решение 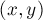 для нашей пары
для нашей пары 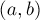 :
:
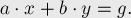
Для этого преобразуем величину 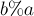 :
:
![b \% a = b - \left\lfloor \frac{b}{a} \right\rflo[...]](../tex2png/cache/3e68805cc79ea5414e08b9f791fc4fd4.png)
Подставим это в приведённое выше выражение с 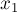 и
и 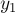 и получим:
и получим:
![g = (b \% a) \cdot x_1 + a \cdot y_1 = \left( b -[...]](../tex2png/cache/326b7a89189c57b2670ac7563f0177fb.png)
и, выполняя перегруппировку слагаемых, получаем:
![g = b \cdot x_1 + a \cdot \left( y_1 - \left\lflo[...]](../tex2png/cache/c74de2715bd7357f9533f732c7ff81ac.png)
Сравнивая это с исходным выражением над неизвестными  и
и  , получаем требуемые выражения:
, получаем требуемые выражения:
![\cases{
x = y_1 - \left\lfloor \frac{b}{a} \righ[...]](../tex2png/cache/3dfc98f04e6ab348ad99ff3d6eee24cc.png)
Реализация
int gcd (int a, int b, int & x, int & y) { if (a == 0) { x = 0; y = 1; return b; } int x1, y1; int d = gcd (b%a, a, x1, y1); x = y1 - (b / a) * x1; y = x1; return d; }
Это рекурсивная функция, которая по-прежнему возвращает значение НОД от чисел  и
и  , но помимо этого — также искомые коэффициенты
, но помимо этого — также искомые коэффициенты  и
и  в виде параметров функции, передающихся по ссылкам.
в виде параметров функции, передающихся по ссылкам.
База рекурсии — случай 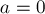 . Тогда НОД равен
. Тогда НОД равен  , и, очевидно, требуемые коэффициенты
, и, очевидно, требуемые коэффициенты  и
и  равны
равны 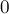 и
и  соответственно. В остальных случаях работает обычное решение, а коэффициенты пересчитываются по вышеописанным формулам.
соответственно. В остальных случаях работает обычное решение, а коэффициенты пересчитываются по вышеописанным формулам.
Расширенный алгоритм Евклида в такой реализации работает корректно даже для отрицательных чисел.
Литература