добавлено: 11 Jul 2008 10:53
редактировано: 6 Sep 2012 21:57

Китайская теорема об остатках

Формулировка

В своей современной формулировке теорема звучит так:

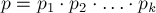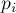Пусть $p = p_1 \cdot p_2 \cdot \ldots \cdot p_k$ , где $p_i$ — попарно взаимно простые числа.

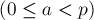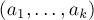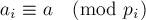Поставим в соответствие произвольному числу $a$ $(0 \le a < p)$ кортеж $(a_1, \ldots, a_k)$ , где $a_i \equiv a \pmod {p_i}$ :

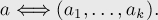
$a \Longleftrightarrow (a_1, \ldots, a_k).$

Тогда это соответствие (между числами и кортежами) будет являться взаимно однозначным. И, более того, операции, выполняемые над числом $a$ , можно эквивалентно выполнять над соответствующими элементами кортежами — путём независимого выполнения операций над каждым компонентом.

Т.е., если

$a \Longleftrightarrow \Big( a_1, \ldots, a_k \Big[...]$
$b \Longleftrightarrow \Big( b_1, \ldots, b_k \Big[...]$

то справедливо:

${(a+b) \pmod p} \Longleftrightarrow \Big( {(a_1+b[...]$
${(a-b) \pmod p} \Longleftrightarrow \Big( {(a_1-b[...]$
${(a \cdot b) \pmod p} \Longleftrightarrow \Big( {[...]$

В своей первоначальной формулировке эта теорема была доказана китайским математиком Сунь-Цзы приблизительно в 100 г. н.э. А именно, он показал в частном случае эквивалентность решения системы модулярных уравнений и решения одного модулярного уравнения (см. следствие 2 ниже).

Следствие 1

Система модулярных уравнений:

$\cases{ {x \equiv a_1 \pmod {p_1}}, \cr \ldots,[...]$

имеет единственное решение по модулю $p$ .

(как и выше, 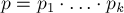$p = p_1 \cdot \ldots \cdot p_k$ , числа 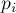$p_i$ попарно взаимно просты, а набор 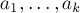$a_1, \ldots, a_k$ — произвольный набор целых чисел)

Следствие 2

Следствием является связь между системой модулярных уравнений и одним соответствующим модулярным уравнением:

Уравнение:

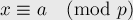
$x \equiv a \pmod p$

эквивалентно системе уравнений:

$\cases{ {x \equiv a \pmod {p_1}}, \cr \ldots, \[...]$

(как и выше, предполагается, что 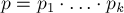$p = p_1 \cdot \ldots \cdot p_k$ , числа 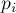$p_i$ попарно взаимно просты, а $a$ — произвольное целое число)

Алгоритм Гарнера

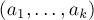Из китайской теоремы об остатках следует, что можно заменять операции над числами операциями над кортежами. Напомним, каждому числу $a$ ставится в соответствие кортеж $(a_1, \ldots, a_k)$ , где:

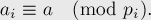
${ a_i \equiv a \pmod {p_i} } .$

Это может найти широкое применение на практике (помимо непосредственного применения для восстановления числа по его остаткам по различным модулям), поскольку мы таким образом можем заменять операции в длинной арифметике операциями с массивом "коротких" чисел. Скажем, массива из 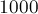$1000$ элементов "хватит" на числа примерно с 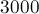$3000$ знаками (если выбрать в качестве 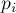$p_i$ -ых первые 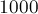$1000$ простых); а если выбирать в качестве 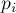$p_i$ -ых простые около миллиарда, то тогда хватит уже на число с примерно 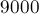$9000$ знаками. Но, разумеется, тогда нужно научиться восстанавливать число $a$ по этому кортежу. 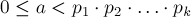Из следствия 1 видно, что такое восстановление возможно, и притом единственно (при условии $0 \le a < p_1 \cdot p_2 \cdot \ldots \cdot p_k$ ). Алгоритм Гарнера и является алгоритмом, позволяющим выполнить это восстановление, причём достаточно эффективно.

Будем искать решение в виде:

$a = x_1 + x_2 \cdot p_1 + x_3 \cdot p_1 \cdot p_2[...]$

т.е. в смешанной системе счисления с весами разрядов 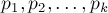$p_1, p_2, \ldots, p_k$ .

Обозначим через 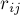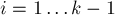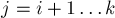$r_{ij}$ ( $i=1 \ldots k-1$ , $j=i+1 \ldots k$ ) число, являющееся обратным для 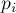$p_i$ по модулю 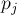$p_j$ (нахождение обратных элементов в кольце по модулю описано здесь:

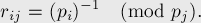
$r_{ij} = (p_i) ^ {-1} \pmod {p_j} .$

Подставим выражение $a$ в смешанной системе счисления в первое уравнение системы, получим:

$a_1 \equiv x_1.$

Подставим теперь выражение во второе уравнение:

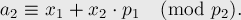
$a_2 \equiv x_1 + x_2 \cdot p_1 \pmod {p_2}.$

Преобразуем это выражение, отняв от обеих частей 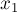$x_1$ и разделив на $p_1$ :

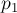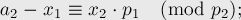
$a_2 - x_1 \equiv x_2 \cdot p_1 \pmod {p_2};$
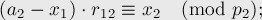
$(a_2 - x_1) \cdot r_{12} \equiv x_2 \pmod {p_2};$
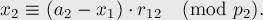
$x_2 \equiv (a_2 - x_1) \cdot r_{12} \pmod {p_2}.$

Подставляя в третье уравнение, аналогичным образом получаем:

$a_3 \equiv { x_1 + x_2 \cdot p_1 + x_3 \cdot p_1 [...]$
$(a_3 - x_1) \cdot r_{13} \equiv x_2 + x_3 \cdot p[...]$
$((a_3 - x_1) \cdot r_{13} - x_2) \cdot r_{23} \eq[...]$
$x_3 \equiv ((a_3 - x_1) \cdot r_{13} - x_2) \cdot[...]$

Уже достаточно ясно видна закономерность, которую проще всего выразить кодом:

for (int i=0; i<k; ++i) {
	x[i] = a[i];
	for (int j=0; j<i; ++j) {
		x[i] = r[j][i] * (x[i] - x[j]);
 
		x[i] = x[i] % p[i];
		if (x[i] < 0)  x[i] += p[i];
	}
}

Итак, мы научились вычислять коэффициенты 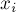$x_i$ за время $O (k^2)$ , сам же ответ — число $a$ — можно восстановить по формуле:

$a = x_1 + x_2 \cdot p_1 + x_3 \cdot p_1 \cdot p_2[...]$

Стоит заметить, что на практике почти всегда вычислять ответ нужно с помощью Длинной арифметики, но при этом сами коэффициенты 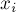$x_i$ по-прежнему вычисляются на встроенных типах, а потому весь алгоритм Гарнера является весьма эффективным.

Реализация алгоритма Гарнера

Удобнее всего реализовывать этот алгоритм на языке Java, поскольку она содержит стандартную длинную арифметику, а потому не возникает никаких проблем с переводом числа из модульной системы в обычное число (используется стандартный класс BigInteger).

Приведённая ниже реализация алгоритма Гарнера поддерживает сложение, вычитание и умножение, причём поддерживает работу с отрицательными числами (об этом см. пояснения после кода). Реализован перевод числа обычного десятичкого представления в модулярную систему и наоборот.

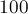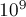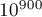В данном примере берутся $100$ простых после $10^9$ , что позволяет работать с числами до примерно $10^{900}$ .

final int SZ = 100;
int pr[] = new int[SZ];
int r[][] = new int[SZ][SZ];
 
void init() {
	for (int x=1000*1000*1000, i=0; i<SZ; ++x)
		if (BigInteger.valueOf(x).isProbablePrime(100))
			pr[i++] = x;
 
	for (int i=0; i<SZ; ++i)
		for (int j=i+1; j<SZ; ++j)
			r[i][j] = BigInteger.valueOf( pr[i] ).modInverse(
					BigInteger.valueOf( pr[j] ) ).intValue();
}
 
 
class Number {
 
	int a[] = new int[SZ];
 
	public Number() {
	}
 
	public Number (int n) {
		for (int i=0; i<SZ; ++i)
			a[i] = n % pr[i];
	}
 
	public Number (BigInteger n) {
		for (int i=0; i<SZ; ++i)
			a[i] = n.mod( BigInteger.valueOf( pr[i] ) ).intValue();
	}
 
	public Number add (Number n) {
		Number result = new Number();
		for (int i=0; i<SZ; ++i)
			result.a[i] = (a[i] + n.a[i]) % pr[i];
		return result;
	}
 
	public Number subtract (Number n) {
		Number result = new Number();
		for (int i=0; i<SZ; ++i)
			result.a[i] = (a[i] - n.a[i] + pr[i]) % pr[i];
		return result;
	}
 
	public Number multiply (Number n) {
		Number result = new Number();
		for (int i=0; i<SZ; ++i)
			result.a[i] = (int)( (a[i] * 1l * n.a[i]) % pr[i] );
		return result;
	}
 
	public BigInteger bigIntegerValue (boolean can_be_negative) {
		BigInteger result = BigInteger.ZERO,
			mult = BigInteger.ONE;
		int x[] = new int[SZ];
		for (int i=0; i<SZ; ++i) {
			x[i] = a[i];
			for (int j=0; j<i; ++j) {
				long cur = (x[i] - x[j]) * 1l * r[j][i];
				x[i] = (int)( (cur % pr[i] + pr[i]) % pr[i] );					
			}
			result = result.add( mult.multiply( BigInteger.valueOf( x[i] ) ) );
			mult = mult.multiply( BigInteger.valueOf( pr[i] ) );
		}
 
		if (can_be_negative)
			if (result.compareTo( mult.shiftRight(1) ) >= 0)
				result = result.subtract( mult );
 
		return result;
	}
}

О поддержке отрицательных чисел следует сказать особо (флаг 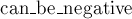$\rm can\_be\_negative$ функции 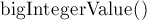${\rm bigIntegerValue}()$ ). Сама модулярная схема не предполагает различий между положительными и отрицательными числами. Однако можно заметить, что, если в конкретной задаче ответ по модулю не превосходит половины от произведения всех простых, то положительные числа будут отличаться от отрицательных тем, что положительные числа получатся меньше этой середины, а отрицательные — больше. Поэтому мы после классического алгоритма Гарнера сравниваем результат с серединой, и если он больше, то выводим минус, и инвертируем результат (т.е. отнимаем его от произведения всех простых, и выводим уже его).