MAXimal

добавлено: 8 Sep 2008 22:04
редактировано: 1 Jun 2009 15:46

Количество помеченных графов

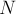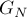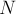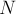Дано число N вершин. Требуется посчитать количество G_N различных помеченных графов с N вершинами (т.е. вершины графа помечены различными числами от 1 до N, и графы сравниваются с учётом этой покраски вершин). Рёбра графа неориентированы, петли и кратные рёбра запрещены.

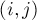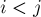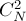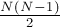Рассмотрим множество всех возможных рёбер графа. Для любого ребра (i,j) положим, что i<j (основываясь на неориентированности графа и отсутствии петель). Тогда множество всех возможных рёбер графа имеет мощность C_N^2, т.е. \frac{ N (N-1) }{ 2 }.

Поскольку любой помеченный граф однозначно определяется своими рёбрами, то количество помеченных графов с 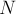N вершинами равно:

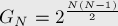
G_N = 2^{ \frac{ N (N-1) }{ 2 } }

Количество связных помеченных графов

По сравнению с предыдущей задачей мы дополнительно накладываем ограничение, что граф должен быть связным.

Обозначим искомое число через 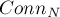Conn_N.

Научимся, наоборот, считать количество несвязных графов; тогда количество связных графов получится как 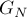G_N минус найденное число. Более того, научимся считать количество корневых (т.е. с выделенной вершиной - корнем) несвязных графов; тогда количество несвязных графов будет получаться из него делением на 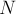N. Заметим, что, так как граф несвязный, то в нём найдётся компонента связности, внутри которой лежит корень, а остальной граф будет представлять собой ещё несколько (как минимум одну) компонент связности.

Переберём количество 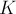K вершин в этой компоненте связности, содержащей корень (очевидно, 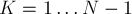K = 1 \ldots N-1), и найдём количество таких графов. Во-первых, мы должны выбрать 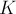K вершин из 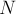N, т.е. ответ умножается на 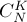C_N^K. Во-вторых, компонента связности с корнем даёт множитель 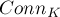Conn_K. В-третьих, оставшийся граф из 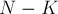N-K вершин является произвольным графом, а потому он даёт множитель 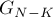G_{N-K}. Наконец, количество способов выделить корень в компоненте связности из 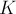K вершин равно 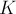K. Итого, при фиксированном 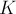K количество корневых несвязных графов равно:

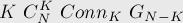
K\ C_N^K\ Conn_K\ G_{N-K}

Значит, количество несвязных графов с 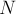N вершинами равно:

\frac{1}{N} \sum_{K=1}^{N-1} K\ C_N^K\ Conn_K\ G_[...]

Наконец, искомое количество связных графов равно:

Conn_N = G_N - \frac{1}{N} \sum_{K=1}^{N-1} K\ C_[...]

Количество помеченных графов с 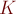K компонентами связности

Основываясь на предыдущей формуле, научимся считать количество помеченных графов с 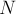N вершинами и 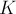K компонентами связности.

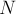Сделать это можно с помощью динамического программирования. Научимся считать D[N][K] — количество помеченных графов с N вершинами и 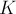K компонентами связности.

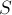Научимся вычислять очередной элемент D[N][K], зная предыдущие значения. Воспользуемся стандартным приёмом при решении таких задач: возьмём вершину с номером 1, она принадлежит какой-то компоненте, вот эту компоненту мы и будем перебирать. Переберём размер S этой компоненты, тогда количество способов выбрать такое множество вершин равно 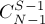C_{N-1}^{S-1} (одну вершину — вершину 1 — перебирать не надо). Количество же способов построить компоненту связности из 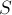S вершин мы уже умеем считать — это 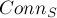Conn_S. После удаления этой компоненты из графа у нас остаётся граф с 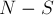N-S вершинами и 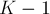K-1 компонентами связности, т.е. мы получили рекуррентную зависимость, по которой можно вычислять значения D[][]:

D[N][K] = \sum_{S=1}^{N} C_{N-1}^{S-1}\ Conn_S\ D[...]

Итого получаем примерно такой код:

int d[n+1][k+1]; // изначально заполнен нулями
d[0][0][0] = 1;
for (int i=1; i<=n; ++i)
	for (int j=1; j<=i && j<=k; ++j)
		for (int s=1; s<=i; ++s)
			d[i][j] += C[i-1][s-1] * conn[s] * d[i-s][j-1];
cout << d[n][k][n];

Разумеется, на практике, скорее всего, нужна будет длинная арифметика.