MAXimal
добавлено: 15 Dec 2011 23:31
редактировано: 16 Dec 2011 0:20
Содержание [скрыть]
Поиск общих касательных к двум окружностям
Даны две окружности. Требуется найти все их общие касательные, т.е. все такие прямые, которые касаются обеих окружностей одновременно.
Описанный алгоритм будет работать также в случае, когда одна (или обе) окружности вырождаются в точки. Таким образом, этот алгоритм можно использовать также для нахождения касательных к окружности, проходящих через заданную точку.
Количество общих касательных
Сразу отметим, что мы не рассматриваем вырожденные случаи: когда окружности совпадают (в этом случае у них бесконечно много общих касательных), или одна окружность лежит внутри другой (в этом случае у них нет общих касательных, или, если окружности касаются, есть одна общая касательная).
В большинстве случаев, две окружности имеют четыре общих касательных.
Если окружности касаются, то у них будет три обших касательных, но это можно понимать как вырожденный случай: так, как будто две касательные совпали.
Более того, описанный ниже алгоритм будет работать и в случае, когда одна или обе окружности имеют нулевой радиус: в этом случае будет, соответственно, две или одна общая касательная.
Подводя итог, мы, за исключением описанных в начале случаев, всегда будем искать четыре касательные. В вырожденных случаях некоторые из них будут совпадать, однако тем не менее эти случаи также будут вписываться в общую картину.
Алгоритм
В целях простоты алгоритма, будем считать, не теряя общности, что центр первой окружности имеет координаты 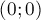 . (Если это не так, то этого можно добиться простым сдвигом всей картины, а после нахождения решения — сдвигом полученных прямых обратно.)
. (Если это не так, то этого можно добиться простым сдвигом всей картины, а после нахождения решения — сдвигом полученных прямых обратно.)
Обозначим через 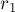 и
и 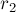 радиусы первой и второй окружностей, а через
радиусы первой и второй окружностей, а через  — координаты центра второй окружности (точка
— координаты центра второй окружности (точка  отлична от начала координат, т.к. мы не рассматриваем случае, когда окружности совпадают, или одна окружность находится внутри другой).
отлична от начала координат, т.к. мы не рассматриваем случае, когда окружности совпадают, или одна окружность находится внутри другой).
Для решения задачи подойдём к ней чисто алгебраически. Нам требуется найти все прямые вида 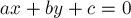 , которые лежат на расстоянии
, которые лежат на расстоянии 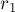 от начала координат, и на расстоянии
от начала координат, и на расстоянии 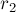 от точки
от точки  . Кроме того, наложим условие нормированности прямой: сумма квадратов коэффициентов
. Кроме того, наложим условие нормированности прямой: сумма квадратов коэффициентов  и
и  должна быть равна единице (это необходимо, иначе одной и той же прямой будет соответствовать бесконечно много представлений вида
должна быть равна единице (это необходимо, иначе одной и той же прямой будет соответствовать бесконечно много представлений вида 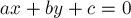 ). Итого получаем такую систему уравнений на искомые
). Итого получаем такую систему уравнений на искомые 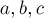 :
:
![\begin{cases}
a^2 + b^2 = 1, \\
| a \cdot 0 + b[...]](../tex2png/cache/7b6e40faec1e1c4756a6d73c01595aa5.png)
Чтобы избавиться от модулей, заметим, что всего есть четыре способа раскрыть модули в этой системе. Все эти способы можно рассмотреть общим случаем, если понимать раскрытие модуля как то, что коэффициент в правой части, возможно, умножается на 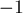 .
.
Иными словами, мы переходим к такой системе:
![\begin{cases}
a^2 + b^2 = 1, \\
c = \pm r_1, \\[...]](../tex2png/cache/a9db587460abb6063fc777ad36052664.png)
Введя обозначения 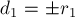 и
и 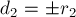 , мы приходим к тому, что четыре раза должны решать систему:
, мы приходим к тому, что четыре раза должны решать систему:
![\begin{cases}
a^2 + b^2 = 1, \\
c = d_1, \\
a [...]](../tex2png/cache/ab045cd38e2e774877384c0bd48adf09.png)
Решение этой системы сводится к решению квадратного уравнения. Мы опустим все громоздкие выкладки, и сразу приведём готовый ответ:
![\begin{cases}
a = \frac{ (d_2-d_1)v_x \pm v_y \s[...]](../tex2png/cache/1d1f86d073e3245eb60eb11a355f43c9.png)
Итого у нас получилось 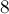 решений вместо
решений вместо 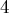 . Однако легко понять, в каком месте возникают лишние решения: на самом деле, в последней системе достаточно брать только одно решение (например, первое). В самом деле, геометрический смысл того, что мы берём
. Однако легко понять, в каком месте возникают лишние решения: на самом деле, в последней системе достаточно брать только одно решение (например, первое). В самом деле, геометрический смысл того, что мы берём 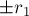 и
и 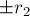 , понятен: мы фактически перебираем, по какую сторону от каждой из окружностей будет прямая. Поэтому два способа, возникающие при решении последней системы, избыточны: достаточно выбрать одно из двух решений (только, конечно, во всех четырёх случаях надо выбрать одно и то же семейство решений).
, понятен: мы фактически перебираем, по какую сторону от каждой из окружностей будет прямая. Поэтому два способа, возникающие при решении последней системы, избыточны: достаточно выбрать одно из двух решений (только, конечно, во всех четырёх случаях надо выбрать одно и то же семейство решений).
Последнее, что мы ещё не рассмотрели — это как сдвигать прямые в том случае, когда первая окружность не находилась изначально в начале координат. Однако здесь всё просто: из линейности уравнения прямой следует, что от коэффициента  надо отнять величину
надо отнять величину 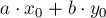 (где
(где 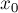 и
и 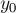 — координаты первоначального центра первой окружности).
— координаты первоначального центра первой окружности).
Реализация
Опишем сначала все необходимые структуры данных и другие вспомогательные определения:
struct pt { double x, y; pt operator- (pt p) { pt res = { x-p.x, y-p.y }; return res; } }; struct circle : pt { double r; }; struct line { double a, b, c; }; const double EPS = 1E-9; double sqr (double a) { return a * a; }
Тогда само решение можно записать таким образом (где основная функция для вызова — вторая; а первая функция — вспомогательная):
void tangents (pt c, double r1, double r2, vector<line> & ans) { double r = r2 - r1; double z = sqr(c.x) + sqr(c.y); double d = z - sqr(r); if (d < -EPS) return; d = sqrt (abs (d)); line l; l.a = (c.x * r + c.y * d) / z; l.b = (c.y * r - c.x * d) / z; l.c = r1; ans.push_back (l); } vector<line> tangents (circle a, circle b) { vector<line> ans; for (int i=-1; i<=1; i+=2) for (int j=-1; j<=1; j+=2) tangents (b-a, a.r*i, b.r*j, ans); for (size_t i=0; i<ans.size(); ++i) ans[i].c -= ans[i].a * a.x + ans[i].b * a.y; return ans; }