MAXimal
добавлено: 10 Jun 2008 18:18
редактировано: 10 Jun 2008 18:40
Содержание [скрыть]
тест BPSW на простоту чисел
Введение
Алгоритм BPSW - это тест числа на простоту. Этот алгоритм назван по фамилиям его изобретателей: Роберт Бэйли (Ballie), Карл Померанс (Pomerance), Джон Селфридж (Selfridge), Сэмюэль Вагстафф (Wagstaff). Алгоритм был предложен в 1980 году. На сегодняшний день к алгоритму не было найдено ни одного контрпримера, равно как и не было найдено доказательство.
Алгоритм BPSW был проверен на всех числах до 1015. Кроме того, контрпример пытались найти с помощью программы PRIMO (см. [6]), основанной на тесте на простоту с помощью эллиптических кривых. Программа, проработав три года, не нашла ни одного контрпримера, на основании чего Мартин предположил, что не существует ни одного BPSW-псевдопростого, меньшего 1010000 (псевдопростое число - составное число, на котором алгоритм даёт результат "простое"). В то же время, Карл Померанс в 1984 году представил эвристическое доказательство того, что существует бесконечное множество BPSW-псевдопростых чисел.
Сложность алгоритма BPSW есть O (log3(N)) битовых операций. Если же сравнивать алгоритм BPSW с другими тестами, например, тестом Миллера-Рабина, то алгоритм BPSW обычно оказывается в 3-7 раз медленнее.
Алгоритм нередко применяется на практике. По-видимому, многие коммерческие математические пакеты, полностью или частично, полагаются на алгоритм BPSW для проверки чисел на простоту.
Краткое описание
Алгоритм имеет несколько различных реализаций, отличающихся друг от друга только деталями. В нашем случае алгоритм имеет вид:
1. Выполнить тест Миллера-Рабина по основанию 2.
2. Выполнить сильный тест Лукаса-Селфриджа, используя последовательности Лукаса с параметрами Селфриджа.
3. Вернуть "простое" только в том случае, когда оба теста вернули "простое".
+0. Кроме того, в начало алгоритма можно добавить проверку на тривиальные делители, скажем, до 1000. Это позволит увеличить скорость работы на составных числах, правда, несколько замедлив алгоритм на простых.
Итак, алгоритм BPSW основывается на следующем:
1. (факт) тест Миллера-Рабина и тест Лукаса-Селфриджа если и ошибаются, то только в одну сторону: некоторые составные числа этими алгоритмами опознаются как простые. В обратную сторону эти алгоритмы не ошибаются никогда.
2. (предположение) тест Миллера-Рабина и тест Лукаса-Селфриджа если и ошибаются, то никогда не ошибаются на одном числе одновременно.
На самом деле, второе предположение вроде бы как и неверно - эвристическое доказательство-опровержение Померанса приведено ниже. Тем не менее, на практике ни одного псевдопростого до сих пор не нашли, поэтому условно можно считать второе предположение верным.
Реализация алгоритмов в данной статье
Все алгоритмы в данной статье будут реализованы на C++. Все программы тестировались только на компиляторе Microsoft C++ 8.0 SP1 (2005), также должны компилироваться на g++.
Алгоритмы реализованы с использованием шаблонов (templates), что позволяет применять их как к встроенным числовым типам, так и собственным классам, реализующим длинную арифметику. [ пока длинная арифметика в статью не входит - TODO ]
В самой статье будут приведены только самые существенные функции, тексты же вспомогательных функций можно скачать в приложении к статье. Здесь будут приведены только заголовки этих функций вместе с комментариями:
//! Модуль 64-битного числа long long abs (long long n); unsigned long long abs (unsigned long long n); //! Возвращает true, если n четное template <class T> bool even (const T & n); //! Делит число на 2 template <class T> void bisect (T & n); //! Умножает число на 2 template <class T> void redouble (T & n); //! Возвращает true, если n - точный квадрат простого числа template <class T> bool perfect_square (const T & n); //! Вычисляет корень из числа, округляя его вниз template <class T> T sq_root (const T & n); //! Возвращает количество бит в числе template <class T> unsigned bits_in_number (T n); //! Возвращает значение k-го бита числа (биты нумеруются с нуля) template <class T> bool test_bit (const T & n, unsigned k); //! Умножает a *= b (mod n) template <class T> void mulmod (T & a, T b, const T & n); //! Вычисляет a^k (mod n) template <class T, class T2> T powmod (T a, T2 k, const T & n); //! Переводит число n в форму q*2^p template <class T> void transform_num (T n, T & p, T & q); //! Алгоритм Евклида template <class T, class T2> T gcd (const T & a, const T2 & b); //! Вычисляет jacobi(a,b) - символ Якоби template <class T> T jacobi (T a, T b) //! Вычисляет pi(b) первых простых чисел. Возвращает вектор с простыми и в pi - pi(b) template <class T, class T2> const std::vector& get_primes (const T & b, T2 & pi); //! Тривиальная проверка n на простоту, перебираются все делители до m. //! Результат: 1 - если n точно простое, p - его найденный делитель, 0 - если неизвестно template <class T, class T2> T2 prime_div_trivial (const T & n, T2 m);
Тест Миллера-Рабина
Я не буду заострять внимание на тесте Миллера-Рабина, поскольку он описывается во многих источниках, в том числе и на русском языке (например. см. [5]).
Замечу лишь, что скорость его работы есть O (log3(N)) битовых операций и приведу готовую реализацию этого алгоритма:
template <class T, class T2>
bool miller_rabin (T n, T2 b)
{
// сначала проверяем тривиальные случаи
if (n == 2)
return true;
if (n < 2 || even (n))
return false;
// проверяем, что n и b взаимно просты (иначе это приведет к ошибке)
// если они не взаимно просты, то либо n не просто, либо нужно увеличить b
if (b < 2)
b = 2;
for (T g; (g = gcd (n, b)) != 1; ++b)
if (n > g)
return false;
// разлагаем n-1 = q*2^p
T n_1 = n;
--n_1;
T p, q;
transform_num (n_1, p, q);
// вычисляем b^q mod n, если оно равно 1 или n-1, то n простое (или псевдопростое)
T rem = powmod (T(b), q, n);
if (rem == 1 || rem == n_1)
return true;
// теперь вычисляем b^2q, b^4q, ... , b^((n-1)/2)
// если какое-либо из них равно n-1, то n простое (или псевдопростое)
for (T i=1; i<p; i++)
{
mulmod (rem, rem, n);
if (rem == n_1)
return true;
}
return false;
}
Сильный тест Лукаса-Селфриджа
Сильный тест Лукаса-Селфриджа состоит из двух частей: алгоритма Селфриджа для вычисления некоторого параметра, и сильного алгоритма Лукаса, выполняемого с этим параметром.
Алгоритм Селфриджа
Среди последовательности 5, -7, 9, -11, 13, ... найти первое число D, для которого J (D, N) = -1 и gcd (D, N) = 1, где J(x,y) - символ Якоби.
Параметрами Селфриджа будут P = 1 и Q = (1 - D) / 4.
Следует заметить, что параметр Селфриджа не существует для чисел, которые являются точными квадратами. Действительно, если число является точным квадратом, то перебор D дойдёт до sqrt(N), на котором окажется, что gcd (D, N) > 1, т.е. обнаружится, что число N составное.
Кроме того, параметры Селфриджа будут вычислены неправильно для чётных чисел и для единицы; впрочем, проверка этих случаев не составит труда.
Таким образом, перед началом алгоритма следует проверить, что число N является нечётным, большим 2, и не является точным квадратом, иначе (при невыполнении хотя бы одного условия) нужно сразу выйти из алгоритма с результатом "составное".
Наконец, заметим, что если D для некоторого числа N окажется слишком большим, то алгоритм с вычислительной точки зрения окажется неприменимым. Хотя на практике такого замечено не было (оказывалось вполне достаточно 4-байтного числа), тем не менее вероятность этого события не следует исключать. Впрочем, например, на отрезке [1; 106] max(D) = 47, а на отрезке [1019; 1019+106] max(D) = 67. Кроме того, Бэйли и Вагстаф в 1980 году аналитически доказали это наблюдение (см. Ribenboim, 1995/96, стр. 142).
Сильный алгоритм Лукаса
Параметрами алгоритма Лукаса являются числа D, P и Q такие, что D = P2 - 4*Q ? 0, и P > 0.
(нетрудно заметить, что параметры, вычисленные по алгоритму Селфриджа, удовлетворяют этим условиям)
Последовательности Лукаса - это последовательности Uk и Vk, определяемые следующим образом:
U0 = 0 U1 = 1 Uk = P Uk-1 - Q Uk-2 V0 = 2 V1 = P Vk = P Vk-1 - Q Vk-2
Далее, пусть M = N - J (D, N).
Если N простое, и gcd (N, Q) = 1, то имеем:
UM = 0 (mod N)
В частности, когда параметры D, P, Q вычислены алгоритмом Селфриджа, имеем:
UN+1 = 0 (mod N)
Обратное, вообще говоря, неверно. Тем не менее, псевдопростых чисел при данном алгоритме оказывается не очень много, на чём, собственно, и основывается алгоритм Лукаса.
Итак, алгоритм Лукаса заключается в вычислении UM и сравнении его с нулём.
Далее, необходимо найти какой-то способ ускорения вычисления UK, иначе, понятно, никакого практического смысла в этом алгоритма не было бы.
Имеем:
Uk = (ak - bk) / (a - b), Vk = ak + bk,
где a и b - различные корни квадратного уравнения x2 - P x + Q = 0.
Теперь следующие равенства можно доказать элементарно:
U2k = Uk Vk (mod N) V2k = Vk2 - 2 Qk (mod N)
Теперь, если представить M = E 2T, где E - нечётное число, то легко получить:
UM = UE VE V2E V4E ... V2T-2E V2T-1E = 0 (mod N),
и хотя бы один из множителей равен нулю по модулю N.
Понятно, что достаточно вычислить UE и VE, а все последующие множители V2E V4E ... V2T-2E V2T-1E можно получить уже из них.
Таким образом, осталось научиться быстро вычислять UE и VE для нечётного E.
Сначала рассмотрим следующие формулы для сложения членов последовательностей Лукаса:
Ui+j = (Ui Vj + Uj Vi) / 2 (mod N) Vi+j = (Vi Vj + D Ui Uj) / 2 (mod N)
Следует обратить внимание, что деление выполняется в поле (mod N).
Формулы эти доказываются очень просто, и здесь их доказательство опущено.
Теперь, обладая формулами для сложения и для удвоения членов последовательностей Лукаса, понятен и способ ускорения вычисления UE и VE.
Действительно, рассмотрим двоичную запись числа E. Положим сначала результат - UE и VE - равными, соответственно, U1 и V1. Пройдёмся по всем битам числа E от более младших к более старшим, пропустив только самый первый бит (начальный член последовательности). Для каждого i-го бита будем вычислять U2 i и V2 i из предыдущих членов с помощью формул удвоения. Кроме того, если текущий i-ый бит равен единице, то к ответу будем прибавлять текущие U2 i и V2 i с помощью формул сложения. По окончании алгоритма, выполняющегося за O (log(E)), мы получим искомые UE и VE.
Если UE или VE оказались равными нулю (mod N), то число N простое (или псевдопростое). Если они оба отличны от нуля, то вычисляем V2E, V4E, ... V2T-2E, V2T-1E. Если хотя бы один из них сравним с нулём по модулю N, то число N простое (или псевдопростое). Иначе число N составное.
Обсуждение алгоритма Селфриджа
Теперь, когда мы рассмотрели алгоритм Лукаса, можно более подробно остановиться на его параметрах D,P,Q, одним из способов получения которых и является алгоритм Селфриджа.
Напомним базовые требования к параметрам:
P > 0, D = P2 - 4*Q ? 0.
Теперь продолжим изучение этих параметров.
D не должно быть точным квадратом (mod N).
Действительно, иначе получим:
D = b2, отсюда J(D,N) = 1, P = b + 2, Q = b + 1, отсюда Un-1 = (Qn-1 - 1) / (Q - 1).
Т.е. если D - точный квадрат, то алгоритм Лукаса становится практически обычным вероятностным тестом.
Один из лучших способов избежать подобного - потребовать, чтобы J(D,N) = -1.
Например, можно выбрать первое число D из последовательности 5, -7, 9, -11, 13, ..., для которого J(D,N) = -1. Также пусть P = 1. Тогда Q = (1 - D) / 4. Этот способ был предложен Селфриджем.
Впрочем, имеются и другие способы выбора D. Можно выбирать его из последовательности 5, 9, 13, 17, 21, ... Также пусть P - наименьшее нечётное, привосходящее sqrt(D). Тогда Q = (P2 - D) / 4.
Понятно, что от выбора конкретного способа вычисления параметров Лукаса зависит и его результат - псевдопростые могут отличаться при различных способах выбора параметра. Как показала практика, алгоритм, предложенный Селфриджем, оказался очень удачным: все псевдопростые Лукаса-Селфриджа не являются псевдопростыми Миллера-Рабина, по крайней мере, ни одного контрпримера найдено не было.
Реализация сильного алгоритма Лукаса-Селфриджа
Теперь осталось только реализовать алгоритм:
template <class T, class T2>
bool lucas_selfridge (const T & n, T2 unused)
{
// сначала проверяем тривиальные случаи
if (n == 2)
return true;
if (n < 2 || even (n))
return false;
// проверяем, что n не является точным квадратом, иначе алгоритм даст ошибку
if (perfect_square (n))
return false;
// алгоритм Селфриджа: находим первое число d такое, что:
// jacobi(d,n)=-1 и оно принадлежит ряду { 5,-7,9,-11,13,... }
T2 dd;
for (T2 d_abs = 5, d_sign = 1; ; d_sign = -d_sign, ++++d_abs)
{
dd = d_abs * d_sign;
T g = gcd (n, d_abs);
if (1 < g && g < n)
// нашли делитель - d_abs
return false;
if (jacobi (T(dd), n) == -1)
break;
}
// параметры Селфриджа
T2
p = 1,
q = (p*p - dd) / 4;
// разлагаем n+1 = d*2^s
T n_1 = n;
++n_1;
T s, d;
transform_num (n_1, s, d);
// алгоритм Лукаса
T
u = 1,
v = p,
u2m = 1,
v2m = p,
qm = q,
qm2 = q*2,
qkd = q;
for (unsigned bit = 1, bits = bits_in_number(d); bit < bits; bit++)
{
mulmod (u2m, v2m, n);
mulmod (v2m, v2m, n);
while (v2m < qm2)
v2m += n;
v2m -= qm2;
mulmod (qm, qm, n);
qm2 = qm;
redouble (qm2);
if (test_bit (d, bit))
{
T t1, t2;
t1 = u2m;
mulmod (t1, v, n);
t2 = v2m;
mulmod (t2, u, n);
T t3, t4;
t3 = v2m;
mulmod (t3, v, n);
t4 = u2m;
mulmod (t4, u, n);
mulmod (t4, (T)dd, n);
u = t1 + t2;
if (!even (u))
u += n;
bisect (u);
u %= n;
v = t3 + t4;
if (!even (v))
v += n;
bisect (v);
v %= n;
mulmod (qkd, qm, n);
}
}
// точно простое (или псевдо-простое)
if (u == 0 || v == 0)
return true;
// довычисляем оставшиеся члены
T qkd2 = qkd;
redouble (qkd2);
for (T2 r = 1; r < s; ++r)
{
mulmod (v, v, n);
v -= qkd2;
if (v < 0) v += n;
if (v < 0) v += n;
if (v >= n) v -= n;
if (v >= n) v -= n;
if (v == 0)
return true;
if (r < s-1)
{
mulmod (qkd, qkd, n);
qkd2 = qkd;
redouble (qkd2);
}
}
return false;
}
Код BPSW
Теперь осталось просто скомбинировать результаты всех 3 тестов: проверка на небольшие тривиальные делители, тест Миллера-Рабина, сильный тест Лукаса-Селфриджа.
template <class T>
bool baillie_pomerance_selfridge_wagstaff (T n)
{
// сначала проверяем на тривиальные делители - например, до 29
int div = prime_div_trivial (n, 29);
if (div == 1)
return true;
if (div > 1)
return false;
// тест Миллера-Рабина по основанию 2
if (!miller_rabin (n, 2))
return false;
// сильный тест Лукаса-Селфриджа
return lucas_selfridge (n, 0);
}
Отсюда можно скачать программу (исходник + exe), содержащую полную реализацию теста BPSW. [77 КБ]
Краткая реализация
Длину кода можно значительно уменьшить в ущерб универсальности, отказавшись от шаблонов и различных вспомогательных функций.
const int trivial_limit = 50;
int p[1000];
int gcd (int a, int b) {
return a ? gcd (b%a, a) : b;
}
int powmod (int a, int b, int m) {
int res = 1;
while (b)
if (b & 1)
res = (res * 1ll * a) % m, --b;
else
a = (a * 1ll * a) % m, b >>= 1;
return res;
}
bool miller_rabin (int n) {
int b = 2;
for (int g; (g = gcd (n, b)) != 1; ++b)
if (n > g)
return false;
int p=0, q=n-1;
while ((q & 1) == 0)
++p, q >>= 1;
int rem = powmod (b, q, n);
if (rem == 1 || rem == n-1)
return true;
for (int i=1; i<p; ++i) {
rem = (rem * 1ll * rem) % n;
if (rem == n-1) return true;
}
return false;
}
int jacobi (int a, int b)
{
if (a == 0) return 0;
if (a == 1) return 1;
if (a < 0)
if ((b & 2) == 0)
return jacobi (-a, b);
else
return - jacobi (-a, b);
int a1=a, e=0;
while ((a1 & 1) == 0)
a1 >>= 1, ++e;
int s;
if ((e & 1) == 0 || (b & 7) == 1 || (b & 7) == 7)
s = 1;
else
s = -1;
if ((b & 3) == 3 && (a1 & 3) == 3)
s = -s;
if (a1 == 1)
return s;
return s * jacobi (b % a1, a1);
}
bool bpsw (int n) {
if ((int)sqrt(n+0.0) * (int)sqrt(n+0.0) == n) return false;
int dd=5;
for (;;) {
int g = gcd (n, abs(dd));
if (1<g && g<n) return false;
if (jacobi (dd, n) == -1) break;
dd = dd<0 ? -dd+2 : -dd-2;
}
int p=1, q=(p*p-dd)/4;
int d=n+1, s=0;
while ((d & 1) == 0)
++s, d>>=1;
long long u=1, v=p, u2m=1, v2m=p, qm=q, qm2=q*2, qkd=q;
for (int mask=2; mask<=d; mask<<=1) {
u2m = (u2m * v2m) % n;
v2m = (v2m * v2m) % n;
while (v2m < qm2) v2m += n;
v2m -= qm2;
qm = (qm * qm) % n;
qm2 = qm * 2;
if (d & mask) {
long long t1 = (u2m * v) % n, t2 = (v2m * u) % n,
t3 = (v2m * v) % n, t4 = (((u2m * u) % n) * dd) % n;
u = t1 + t2;
if (u & 1) u += n;
u = (u >> 1) % n;
v = t3 + t4;
if (v & 1) v += n;
v = (v >> 1) % n;
qkd = (qkd * qm) % n;
}
}
if (u==0 || v==0) return true;
long long qkd2 = qkd*2;
for (int r=1; r<s; ++r) {
v = (v * v) % n - qkd2;
if (v < 0) v += n;
if (v < 0) v += n;
if (v >= n) v -= n;
if (v >= n) v -= n;
if (v == 0) return true;
if (r < s-1) {
qkd = (qkd * 1ll * qkd) % n;
qkd2 = qkd * 2;
}
}
return false;
}
bool prime (int n) { // эту функцию нужно вызывать для проверки на простоту
for (int i=0; i<trivial_limit && p[i]<n; ++i)
if (n % p[i] == 0)
return false;
if (p[trivial_limit-1]*p[trivial_limit-1] >= n)
return true;
if (!miller_rabin (n))
return false;
return bpsw (n);
}
void prime_init() { // вызвать до первого вызова prime() !
for (int i=2, j=0; j<trivial_limit; ++i) {
bool pr = true;
for (int k=2; k*k<=i; ++k)
if (i % k == 0)
pr = false;
if (pr)
p[j++] = i;
}
}
Эвристическое доказательство-опровержение Померанса
Померанс в 1984 году предложил следующее эвристическое доказательство.
Утверждение: Количество BPSW-псевдопростых от 1 до X больше X1-a для любого a > 0.
Доказательство.
Пусть k > 4 - произвольное, но фиксированное число. Пусть T - некоторое большое число.
Пусть Pk(T) - множество таких простых p в интервале [T; Tk], для которых:
(1) p = 3 (mod 8), J(5,p) = -1
(2) число (p-1)/2 не является точным квадратом
(3) число (p-1)/2 составлено исключительно из простых q < T
(4) число (p-1)/2 составлено исключительно из таких простых q, что q = 1 (mod 4)
(5) число (p+1)/4 не является точным квадратом
(6) число (p+1)/4 составлено исключительно из простых d < T
(7) число (p+1)/4 составлено исключительно из таких простых d, что q = 3 (mod 4)
Понятно, что приблизительно 1/8 всех простых в отрезке [T; Tk] удовлетворяет условию (1). Также можно показать, что условия (2) и (5) сохраняют некоторую часть чисел. Эвристически, условия (3) и (6) также позволяют нам оставить некоторую часть чисел из отрезка (T; Tk). Наконец, событие (4) обладает вероятностью (c (log T)-1/2), так же как и событие (7). Таким образом, мощность множества Pk(T) прблизительно равна при T -> oo
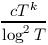
где c - некоторая положительная константа, зависящая от выбора k.
Теперь мы можем построить число n, не являющееся точным квадратом, составленное из l простых из Pk(T), где l нечётно и меньше T2 / log(Tk). Количество способов выбрать такое число n есть примерно
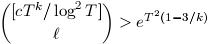
для большого T и фиксированного k. Кроме того, каждое такое число n меньше eT2.
Обозначим через Q1 произведение простых q < T, для которых q = 1 (mod 4), а через Q3 - произведение простых q < T, для которых q = 3 (mod 4). Тогда gcd (Q1, Q3) = 1 и Q1 Q3 ? eT. Таким образом, количество способов выбрать n с дополнительными условиями
n = 1 (mod Q1), n = -1 (mod Q3)
должно быть, эвристически, как минимум
eT 2 (1 - 3 / k) / e 2T > eT 2 (1 - 4 / k)
для большого T.
Но каждое такое n - это контрпример к тесту BPSW. Действительно, n будет числом Кармайкла (т.е. числом, на котором тест Миллера-Рабина будет ошибаться при любом основании), поэтому оно автоматически будет псевдопростым по основанию 2. Поскольку n = 3 (mod 8) и каждое p | n равно 3 (mod 8), очевидно, что n также будет сильным псевдопростым по основанию 2. Поскольку J(5,n) = -1, то каждое простое p | n удовлетворяет J(5,p) = -1, и так как p+1 | n+1 для любого простого p | n, отсюда следует, что n - псевдопростое Лукаса для любого теста Лукаса с дискриминантом 5.
Таким образом, мы показали, что для любого фиксированного k и всех больших T, будет как минимум eT 2 (1 - 4 / k) контрпримеров к тесту BPSW среди чисел, меньших eT 2. Теперь, если мы положим x = eT 2, будет как минимум x1 - 4 / k контрпримеров, меньших x. Поскольку k - случайное число, то наше доказательство означает, что количество контрпримеров, меньших x, есть число, большее x1-a для любого a > 0.
Практические испытания теста BPSW
В этом разделе будут рассмотрены результаты, полученные мной в результате тестирования моей реализации теста BPSW. Все испытания проводились на встроенном типе - 64-битном числе long long. Длинная арифметика не тестировалась.
Тестирования проводились на компьютере с процессором Celeron 1.3 GHz.
Все времена даны в микросекундах (10 -6 сек).
Среднее время работы на отрезке чисел в зависимости от предела тривиального перебора
Имеется в виду параметр, передаваемый функции prime_div_trivial(), который в коде выше равен 29.
Скачать тестовую программу (исходник и exe-файл). [83 КБ]
Если запускать тест на всех нечетных числах из отрезка, то результаты получаются такими:
| начало отрезка | конец отрезка | предел > перебора > | 0 | 102 | 103 | 104 | 105 |
|---|---|---|---|---|---|---|---|
| 1 | 105 | 8.1 | 4.5 | 0.7 | 0.7 | 0.9 | |
| 106 | 106+105 | 12.8 | 6.8 | 7.0 | 1.6 | 1.6 | |
| 109 | 109+105 | 28.4 | 12.6 | 12.1 | 17.0 | 17.1 | |
| 1012 | 1012+105 | 41.5 | 16.5 | 15.3 | 19.4 | 54.4 | |
| 1015 | 1015+105 | 66.7 | 24.4 | 21.1 | 24.8 | 58.9 |
Если запускать тест только на простых числах из отрезка, то скорость работы такова:
| начало отрезка | конец отрезка | предел > перебора > | 0 | 102 | 103 | 104 | 105 |
|---|---|---|---|---|---|---|---|
| 1 | 105 | 42.9 | 40.8 | 3.1 | 4.2 | 4.2 | |
| 106 | 106+105 | 75.0 | 76.4 | 88.8 | 13.9 | 15.2 | |
| 109 | 109+105 | 186.5 | 188.5 | 201.0 | 294.3 | 283.9 | |
| 1012 | 1012+105 | 288.3 | 288.3 | 302.2 | 387.9 | 1069.5 | |
| 1015 | 1015+105 | 485.6 | 489.1 | 496.3 | 585.4 | 1267.4 |
Таким образом, оптимально выбирать предел тривиального перебора равным 100 или 1000.
Для всех следующих тестов я выбрал предел 1000.
Среднее время работы на отрезке чисел
Теперь, когда мы выбрали предел тривиального перебора, можно более точно протестировать скорость работы на различных отрезках.
Скачать тестовую программу (исходник и exe-файл). [83 КБ]
| начало отрезка | конец отрезка | время работы на нечетных числах | время работы на простых числах |
|---|---|---|---|
| 1 | 105 | 1.2 | 4.2 |
| 106 | 106+105 | 13.8 | 88.8 |
| 107 | 107+105 | 16.8 | 115.5 |
| 108 | 108+105 | 21.2 | 164.8 |
| 109 | 109+105 | 24.0 | 201.0 |
| 1010 | 1010+105 | 25.2 | 225.5 |
| 1011 | 1011+105 | 28.4 | 266.5 |
| 1012 | 1012+105 | 30.4 | 302.2 |
| 1013 | 1013+105 | 33.0 | 352.2 |
| 1014 | 1014+105 | 37.5 | 424.3 |
| 1015 | 1015+105 | 42.3 | 499.8 |
| 1016 | 1015+105 | 46.5 | 553.6 |
| 1017 | 1015+105 | 48.9 | 621.1 |
Или, в виде графика, приблизительное время работы теста BPSW на одном числе:
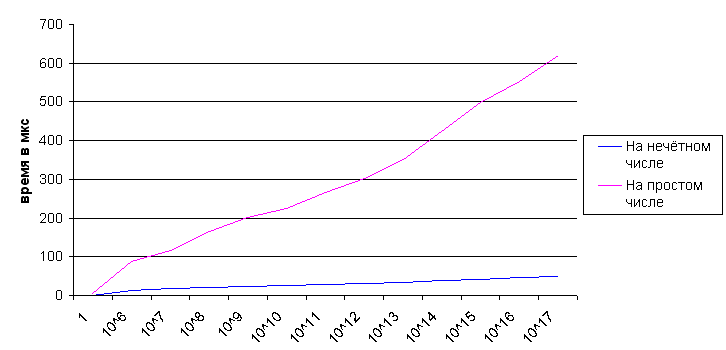
То есть мы получили, что на практике, на небольших числах (до 1017), алгоритм работает за O (log N). Это объясняется тем, что для встроенного типа int64 операция деления выполняется за O(1), т.е. сложность деления не зависисит от количества битов в числе.
Если же применить тест BPSW к длинной арифметике, то ожидается, что он будет работать как раз за O (log3(N)). [ TODO ]
Приложение. Все программы
Скачать все программы из данной статьи. [242 КБ]
Литература
Использованная мной литература, полностью доступная в Интернете:
- Robert Baillie; Samuel S. Wagstaff
Lucas pseudoprimes
Math. Comp. 35 (1980) 1391-1417
mpqs.free.fr/LucasPseudoprimes.pdf
- Daniel J. Bernstein
Distinguishing prime numbers from composite numbers: the state of the art in 2004
Math. Comp. (2004)
cr.yp.to/primetests/prime2004-20041223.pdf
- Richard P. Brent
Primality Testing and Integer Factorisation
The Role of Mathematics in Science (1990)
wwwmaths.anu.edu.au/~brent/pd/rpb120.pdf
- H. Cohen; H. W. Lenstra
Primality Testing and Jacobi Sums
Amsterdam (1984)
www.openaccess.leidenuniv.nl/bitstream/1887/2136/1/346_065.pdf
- Thomas H. Cormen; Charles E. Leiserson; Ronald L. Rivest
Introduction to Algorithms
[ без ссылки ]
The MIT Press (2001)
- M. Martin
PRIMO - Primality Proving
www.ellipsa.net
- F. Morain
Elliptic curves and primality proving
Math. Comp. 61(203) (1993)
citeseer.ist.psu.edu/rd/43190198%2C72628%2C1%2C0.25%2CDownload/ftp%3AqSqqSqftp.inria.frqSqINRIAqSqpublicationqSqpubli-ps-gzqSqRRqSqRR-1256.ps.gz
- Carl Pomerance
Are there counter-examples to the Baillie-PSW primality test?
Math. Comp. (1984)
www.pseudoprime.com/dopo.pdf
- Eric W. Weisstein
Baillie-PSW primality test
MathWorld (2005)
mathworld.wolfram.com/Baillie-PSWPrimalityTest.html
- Eric W. Weisstein
Strong Lucas pseudoprime
MathWorld (2005)
mathworld.wolfram.com/StrongLucasPseudoprime.html
- Paulo Ribenboim
The Book of Prime Number Records
Springer-Verlag (1989)
[ без ссылки ]
Список других рекомендуемых книг, которых мне не удалось найти в Интернете:
- Zhaiyu Mo; James P. Jones
A new primality test using Lucas sequences
Preprint (1997)
- Hans Riesel
Prime numbers and computer methods for factorization
Boston: Birkhauser (1994)