Троичная сбалансированная система счисления

Троичная сбалансированная система счисления — это нестандартная позиционная система счисления. Основание системы равно 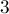$3$ , однако она отличается от обычной троичной системы тем, что цифрами являются 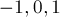$-1, 0, 1$ . Поскольку использовать 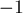$-1$ для одной цифры очень неудобно, то обычно принимают какое-то специальное обозначение. Условимся здесь обозначать минус единицу буквой $z$ .

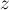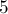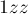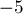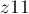Например, число $5$ в троичной сбалансированной системе записывается как $1zz$ , а число $-5$ — как $z11$ . Троичная сбалансированная система счисления позволяет записывать отрицательные числа без записи отдельного знака "минус". Троичная сбалансированная система позволяет дробные числа (например, 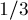$1/3$ записывается как $0.1$ ).

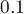Алгоритм перевода

Научимся переводить числа в троичную сбалансированную систему.

Для этого надо сначала перевести число в троичную систему.

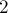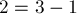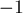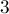Ясно, что теперь нам надо избавиться от цифр $2$ , для чего заметим, что $2 = 3 - 1$ , т.е. мы можем заменить двойку в текущем разряде на $-1$ , при этом увеличив следующий (т.е. слева от него в естественной записи) разряд на $1$ . Если мы будем двигаться по записи справа налево и выполнять вышеописанную операцию (при этом в каких-то разрядах может происходить переполнение больше $3$ , в таком случае, естественно, "сбрасываем" лишние тройки в старший разряд), то придём к троичной сбалансированной записи. Как нетрудно убедиться, то же самое правило верно и для дробных чисел.

Более изящно вышеописанную процедуру можно описать так. Мы берём число в троичной системе счисления, прибавляем к нему бесконечное число 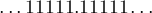$\ldots 11111.11111 \ldots$ , а затем от каждого разряда результата отнимаем единицу (уже безо всяких переносов).

Зная теперь алгоритм перевода из обычной троичной системы в сбалансированную, легко можно реализовать операции сложения, вычитания и деления — просто сводя их к соответствующим операциям над троичными несбалансированными числами.